Introduction aux fonctions affines
Voici un type de fonction usuelle simplissime. La première à être enseignée, avec la fonction linéaire, dès la classe de troisième. Sa représentation graphique est une droite positionnée dans le plan. Niveau de difficulté de cette page : classes de seconde et de premières technologiques.
Présentation
Une fonction affine est définie sur \(\mathbb{R}\) (sauf si elle est appliquée à un problème concret). C'est une fonction qui multiplie tout réel \(x\) par un réel constant \(a\) et lui ajoute le réel constant \(b\). Soit \(f\) une fonction affine. Elle a donc pour modèle l'équation \(f(x)=ax+b\).
On relève le lien avec l'équation réduite d'une droite, \(a\) étant le coefficient directeur de la représentation graphique de \(f\) et \(b\) son ordonnée à l’origine. La courbe représentant une fonction affine (oui, c'est bizarre d'appeler une droite courbe) contient donc le point de coordonnées \((0\,;b)\).
Si \(b=0\), la fonction est linéaire, c'est-à-dire de type \(f(x)=ax\). Sa représentation graphique passe par l’origine du repère et permet de visualiser une parfaite proportionnalité. \(a\) est tout simplement le coefficient de proportionnalité qui permet de passer de \(x\) à \(f(x)\).
Est si c'est \(a\) qui est nul ? Il n'y a plus de direction. \(f(x)=b\). La fonction n'est pas affine mais constante. Son portrait ressemble à un encéphalogramme plat, bref, à une droite horizontale, parallèle à l'axe des abscisses.
Si \(a > 0\) la fonction affine est strictement croissante et si \(a < 0\) elle est strictement décroissante sur \(\mathbb{R}\).
Algébriquement, un coefficient directeur se détermine grâce à deux valeurs choisies arbitrairement et à leurs images calculées. C'est le taux d'accroissement :
\(a = \frac{{f\left( {{x_B}} \right) - f\left( {{x_A}} \right)}}{{{x_B} - {x_A}}}\)
Quant à \(b\), c'est bien sûr \(f(0)\).
Graphiquement, le coefficient \(a\) est la distance verticale qui permet de retrouver la droite lorsqu'on avance \(x\) d’une seule unité. Évidemment, \(a\) est positif lorsque la fonction est croissante et négatif lorsqu'elle est décroissante (voir la page droite dans le plan).
Contrairement à la fonction linéaire, l'affine ne formalise pas une situation de proportionnalité. En revanche, il y a bien proportionnalité des variations, comme le montre la formule du coefficient directeur (accroissement des images proportionnel à celui de la variable \(x\)).
Signe
La racine d'une fonction est la valeur qui l'annule (en l'occurrence \( - \frac{b}{a}\)).
Le signe d'une fonction affine est celui de son coefficient directeur pour les valeurs de \(x\) supérieures à sa racine. C'est évident si l'on se réfère à la représentation graphique.
Exemple : la droite ci-dessous représente la fonction \(f\) définie par \(f(x)=2x+1\). Nous avons \(a=2\). Cette valeur est positive. \(f\) est donc croissante.

Pour les valeurs inférieures à la racine (soit -0,5), la droite est en zone rouge (la fonction est négative), puis pour les valeurs supérieures elle est en zone verte (la fonction est positive, c'est-à-dire du même signe que le coefficient directeur).
Par le calcul, il suffit de résoudre l'équation \(f(x)>0\) pour savoir sur quel intervalle la fonction est positive.
Dérivée (programme de première)
La dérivée d'une fonction affine est égale au coefficient directeur de sa représentation graphique. C'est donc une fonction constante.
Primitive (programme de terminale générale)
Voir les primitives des fonctions usuelles.
Fonction affine par morceaux
Une telle fonction se présente comme une suite d'affines, linéaires ou constantes dont l’expression diffère selon des intervalles. Il est désormais inhabituel que ce type de fonction soit abordé en classe de seconde.
Exemple : \(f(x) = \left| {x + 2} \right| + \left| {x + 1} \right|\) (réalisation avec Sine Qua Non). La fonction \(f\) est continue mais ce n'est pas le cas de toutes les affines par morceaux. Voir d'autres spécimens en pages valeur absolue et fonction valeur absolue.
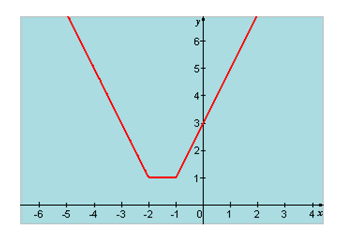
Belle progéniture...
La multiplication de deux fonctions affines se traduit tout simplement par une fonction polynomiale du second degré. Le quotient de deux fonctions affines est une fonction homographique. La composée de deux fonctions affines est elle aussi affine. Si le réel \(x\) est remplacé par un entier naturel \(n\), la fonction est une suite arithmétique.
