Présentation de la fonction racine carrée
La fonction racine carrée est une fonction de référence, dont l’étude est au programme de seconde. Cette page est d’ailleurs rédigée à leur attention, mais plutôt à titre de révision en fin d'année quand toutes les notions sont assimilées.
À savoir
Le symbole de la racine carrée est nommé le radical : \(\sqrt{x}\)
Résumons-nous. La fonction racine carrée a pour ensemble de définition l'intervalle \([0\,;+\infty[.\) Par définition, \(\sqrt{x} = k\) \(\Leftrightarrow\) \(x = k^2\) avec \(x \geqslant 0\) et \(k \geqslant 0.\)
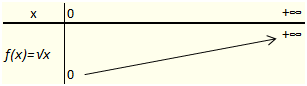
Le sens de variation est assez évident à définir. Plus un nombre positif est grand, plus sa racine carrée l’est aussi. Du coup, le tableau de variation apparaît dans sa redoutable simplicité :
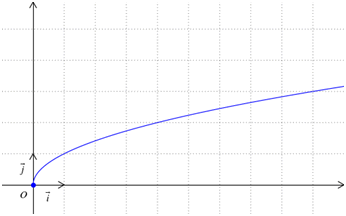
Ci-dessous figure la courbe représentative, réalisée avec WxGéométrie. On constate facilement que la racine de 1 est 1, que celle de 4 est 2 et que celle de 9 est 3. C’est une demi-parabole. Remarquons aussi qu’entre 0 et 1, la racine carrée d’un nombre est supérieure à celui-ci.
Même si ce n’est pas au programme, il peut être utile de savoir qu’une racine carrée est exactement la même chose qu’une puissance 0,5 (par exemple si vous n'avez sous la main qu'un modèle très basique de calculatrice).
Note : la dérivation n'est pas traitée ici puisqu'on ne l'aborde qu'en classe de première.
Exercices
1- Résoudre dans \(\mathbb{R}_+\) : \(3 \sqrt{x} - 1 = 0\) et \(\sqrt{x} \geqslant \frac{2}{3}\)
2- Soit un coût unitaire en euros qui peut être modélisé par la fonction \(c\) définie comme suit (\(x\) représentant des kg produits) : \(c(x) = 50 + 2\sqrt{x-30}\)
La production minimale quotidienne est de 30 kg. Quelle production maximale doit être réalisée pour ne pas dépasser un coût unitaire de 100 € ?
Éléments de correction
1- Équation et inéquation
\(3\sqrt{x} = 1\)
\(\Leftrightarrow \sqrt{x} = \frac{1}{3}\)
\(\Leftrightarrow x = \frac{1}{9}\)
Donc \(S =\{\frac{1}{9}\}\)
\(\sqrt{x} \geqslant \frac{2}{5}\)
\(\Leftrightarrow x \geqslant \frac{4}{25}\)
Donc \(S = [\frac{4}{25}\,; +\infty[.\)
2- Fonction
\(50 + 2\sqrt{x - 30} \geqslant{x - 30} \leqslant 100\)
\(\Leftrightarrow 2\sqrt{x - 30} \leqslant 50\)
\(\Leftrightarrow \sqrt{x - 30} \leqslant 25\)
\(\Leftrightarrow x - 30 \leqslant 625\)
\(\Leftrightarrow x \leqslant 655\)
La production quotidienne ne doit pas dépasser 655 kg.
Exercices supplémentaires
(un peu plus difficiles)
1- Démontrer que la fonction racine carrée est croissante.
2- Soit la fonction \(f\) définie sur \([0\,; +\infty[\) par :
\[f(x) = \frac{1}{\sqrt{x} + \sqrt{x + 1 }}\]
Réécrire \(f(x)\) sans radicaux au dénominateur (car il est habituel de ne pas laisser de radical au numérateur).
Corrigé 1
Soit deux réels positifs \(a\) et \(b,\) avec \(a < b\)
Nous avons donc \(b - a > 0\) et il nous faut prouver que \(f(b) - f(a) > 0.\)
Comme \(a\) et \(b\) sont positifs…
\(b - a\) \(=\) \(\sqrt{b}^2 - \sqrt{a}^2\) \(=\) \((\sqrt{b} + \sqrt{a})(\sqrt{b} - \sqrt{a})\)
Ainsi, l’astuce consiste à utiliser une identité remarquable. Le premier facteur est bien sûr positif puisque c’est la somme de deux nombres positifs. Et le second terme ? Il est du même signe que \((b - a),\) c’est-à-dire positif ! Nous avons bien démontré que \(f(b) - f(a) > 0.\)
Corrigé 2
Pour ôter les radicaux du dénominateur, on utilise la technique des quantités conjuguées (application d’une identité remarquable) :
\(f(x) = \frac{\sqrt{x} - \sqrt{x + 1}}{(\sqrt{x} + \sqrt{x + 1})(\sqrt{x} - \sqrt{x + 1})}\)
\(\Leftrightarrow f(x) = \frac{\sqrt{x} - \sqrt{x + 1}}{x - x - 1}\)
\(\Leftrightarrow f(x) = \sqrt{x + 1 } - \sqrt{x}\)
