Test du coefficient de Spearman
Une corrélation n'est pas forcément linéaire. Pourtant, c'est souvent au modèle linéaire que l'on s'arrête, sans chercher plus loin. Fatale erreur.
Pourquoi ?
Le coefficient de corrélation de Spearman constitue dans certaines situations une alternative intéressante au coefficient de corrélation de Pearson. D’ailleurs, on n’a parfois pas le choix (variables ordinales). Il y a bien le coefficient de Kendall mais, sauf dans les cas où l'on relève beaucoup d'ex-æquo, il semble moins performant que son confrère de Spearman...
Considérons la progression suivante. Elle n'a rien de linéaire. D'ailleurs le coefficient de corrélation linéaire atteint péniblement 0,74. Mais elle est monotone.
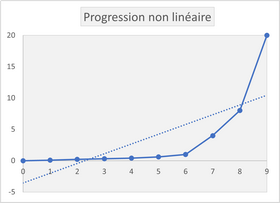
Le coefficient de Spearman rend compte de cette parfaite monotonie.
Formule
Sa formule est particulièrement poétique :
\[\rho = 1 - \frac{6 \sum\limits_{x = 1}^n {d^2_i}}{n^3 - n}\]
Le résultat de ce beau calcul est un nombre compris entre -1 (classements inverses) et 1 (classements identiques), la valeur zéro indiquant que nos deux classements n’ont vraiment rien à voir l’un avec l’autre. Le mécanisme du calcul est détaillé en page de corrélation des rangs.
Un test
Le problème qui va nous tenir en haleine le long de cette page est de savoir à partir de quelles valeurs on va considérer qu’il y a dépendance ou indépendance. Reconnaissons que le thème est pointu, mais il l’est toutefois moins que certains sujets qui ratissent un lectorat largement supérieur à celui de cette page (quelles chaussures a portées telle starlette à telle soirée, tel acteur avait un bouton sur le visage, etc.).

Bref, vous avez sans doute deviné qu’il faut procéder à un test (non paramétrique). Rien de très sorcier, mais c’est loin d’être le test le plus courant. D’ailleurs, la table de ce coefficient est assez rarement publiée.
Très simple à utiliser pour tout statisticien habitué à fréquenter ce genre de document, les valeurs dépendent du nombre d’unités statistiques et du niveau de confiance que l’on se donne.
Voici un tout petit extrait de cette table pour le seuil de confiance habituel de \(95\%.\) Autour d’un effectif d’une centaine, il suffit d’un coefficient supérieur à 0,2 (ou inférieur à -0,2) pour considérer qu’il existe une liaison.
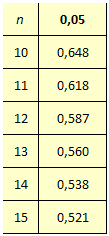
À partir de dix observations, on peut approximer les valeurs de la table en utilisant la statistique suivante :
\[t = \rho \sqrt{\frac{n-2}{1 - \rho}}\]
Cette statistique suit une loi de Student à \(n - 2\) degrés de liberté (source : Statistiques avec Excel de J.-P. Georgin et M. Gouet, PUR 2005, p. 285).
Cependant, ces approximations ne sont utiles que si l’on programme le test. Il est d’ailleurs tout à fait possible de le réaliser avec un tableur. C’est un peu long mais on a l'avantage de maîtriser certaines règles (traitement des ex-æquo, par exemple…).
Exemple
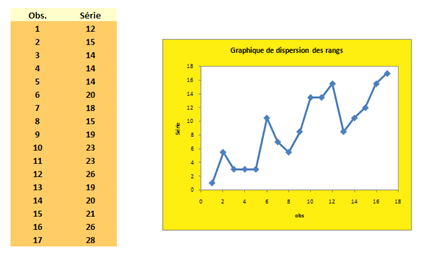
Hypothèse H0 : il n’y a pas de corrélation des rangs.
Hypothèse H1 : il existe une corrélation "monotone".
Premièrement, voyons la sortie de XLSTAT (Tests de corrélation, option Spearman) :

Après observation du graphique, le rejet de H0 semblait de toute façon évident...
Deuxièmement, regardons la sortie du logiciel libre Tanagra (Nonparametric statistics, Spearman’s rho).

On trouve le même coefficient. Un \(\rho\) dissemblable aurait pu s’expliquer par un traitement différent des ex-æquo.
