Initiation à la loi de Benford
Franck Benford (1883-1948), physicien et ingénieur américain, a formalisé une loi de probabilité applicable dans bon nombre de situations concrètes. Elle modélise une situation où les premiers nombres d’une série statistique n’apparaissent pas de façon équiprobable. Le 1 a près d’une chance sur 3 d’être obtenu, suivi du 2, etc. Le 9 est tiré dans moins de \(5\%\) des cas.
Un exemple
Relevons les numéros d’adresse sur les enveloppes dans un centre de tri postal. Nombre d’entre eux commencent par 1. Beaucoup moins commencent par 9.
En effet, une ruelle peut avoir des numéros 1, 2… sans aller jusqu’au 9.
La plupart des rues présentent des numéros 10, 11, 12… mais un peu moins souvent des 20, 21, 22... Ainsi le nombre de numéros d’adresse commençant par 2 est logiquement inférieur au nombre de numéros commençant par 1. Et ainsi de suite. Compte tenu de la longueur des rues, il est moins fréquent d’habiter au 90 ou au 99. Ainsi, pour la plupart des adresses dont le numéro commence par un 9, il s’agit du 9 des unités et occasionnellement celui des dizaines.
Bien sûr, certaines rues sont plus longues avec des numéros supérieurs à 99 mais là encore, le 1 des centaines se rencontre plus souvent que le 2 et ainsi de suite.

Loi de Benford
La loi de Benford fait intervenir le logarithme décimal. Comme nous le verrons, elle peut faire l’objet d’un exercice dans le secondaire en filière générale et une version avec logarithme népérien peut être utilisée.
Soit \(k\) le premier chiffre d’un nombre. La probabilité d’obtenir un nombre commençant par \(k\) est :
\(P(k) = \log_{10}(1 + \frac{1}{k})\)
Ainsi on obtient :
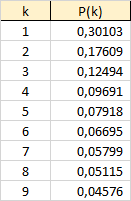
La formule avec logarithmes népériens est équivalente. Elle est juste un peu plus compliquée à écrire :
\(P(k) = \frac{\ln(k + 1) - \ln (k)}{\ln(10)}\)
L’une des applications de cette loi est de détecter les fraudes.
Exercice
Cet exercice est issu de l’épreuve du bac ES de juin 2017 (métropole).
- Dans cet exercice, on considère le premier chiffre des entiers naturels non nuls, en écriture décimale. Par exemple, le premier chiffre de 2017 est 2 et le premier chiffre de 95 est 9.
- Dans certaines circonstances, le premier chiffre d’un nombre aléatoire non nul peut être modélisé par une variable aléatoire \(X\) telle que pour tout entier \(c\) compris entre 1 et 9,
- \[P(X = c) = \frac{\ln(c + 1) - \ln(c)}{\ln(10)}\]
- Cette loi est appelée loi de Benford.
- 1. Que vaut \(P(X = 1)\) ?
- 2. On souhaite examiner si la loi de Benford est un modèle valide dans deux cas particuliers.
- a. Premier cas
- Un fichier statistique de l’INSEE indique la population des communes en France au 1er janvier 2016 (champ : France métropolitaine et départements d’outre-mer de la Guadeloupe, de la Martinique et de la Réunion).
- À partir de ce fichier, on a constaté qu’il y a 36 677 communes habitées. Parmi elles, il y a 11 094 communes dont la population est un nombre qui commence par le chiffre 1.
- Cette observation vous semble-t-elle compatible avec l’affirmation : « le premier chiffre de la population des communes en France au 1er janvier 2016 suit une loi de Benford » ?
- b. Deuxième cas
- Pour chaque candidat au baccalauréat de la session 2017, on considère sa taille en centimètres.
- On désigne par \(X\) la variable aléatoire égale au premier chiffre de la taille en centimètres d’un candidat pris au hasard.
- La loi de Benford vous semble-t-elle adaptée pour \(X\) ?
Corrigé
1- \(P(X = 1) = \frac{\ln(2) - \ln(1)}{\ln(10)} \approx 0,301\) (qui figure dans le tableau plus haut).
2- Cette double question porte sur l’estimation, telle qu’elle était enseignée en terminale à l’époque.
a. Soit la fréquence \(f = \frac{11094}{36677} ≈ 0,3025\)
Ce chiffre est très proche de la valeur théorique. Voyons si ces deux nombres peuvent être considérés comme égaux au seuil de \(95\%.\)
Comme la taille de l’échantillon \(n\) est supérieure à 30, que \(np \geqslant 5\) et \(n(1-p) \geqslant 5\) on peut poser l’intervalle de fluctuation asymptotique au seuil de\(95\ %\) :
\[I = [p - 1,96 \frac{\sqrt{p(1-p)}}{\sqrt{n}}\, ; p + 1,96 \frac{\sqrt{p(1-p)}}{\sqrt{n}}\]
\(p = 0,301\) et \(1 - p = 0,699\)
\( p - 1,96 \frac{\sqrt{p(1-p)}}{\sqrt{n}}\) \(=\) \(0,301 - 1,96 \frac{\sqrt{0,301 × 0,699}}{\sqrt{36677}}\) \(≈\) \(0,296\)
On trouve \(I \approx [0,296\, ; 0,306]\)
Comme \(f ∈ I\) nous concluons que le premier chiffre de la population des communes françaises suit une loi de Benford.
b. L’énoncé ne fournit aucun chiffre. Nous devons répondre à une question de bon sens, sans calcul.
C’est la quasi-totalité des élèves qui ont une taille comprise entre 100 cm et 199 cm. La proportion exacte est inconnue mais en tout cas largement supérieure à \(30,1\%.\)
La loi de Benford ne s’applique évidemment pas.
