Équations différentielles à coefficient constant
Vous savez résoudre une équation différentielle homogène et vous souhaitez aller un peu plus loin. Vous êtes au bon endroit.

Présentation
Soit l'équation différentielle d'ordre 1 : \(y' = ay + b\) (vous l'avez deviné, \(a\) et \(b\) sont des réels et \(a ≠ 0\)).
Les solutions sont du type \(y(x) = ce^{ax} - \frac{b}{a}\) (avec \(c\) constante réelle).
Parmi les solutions, une seule vérifie une condition initiale de type \(y(x_0) = y_0.\)
Par exemple \(y' = 2y - 5\)
En appliquant formule, \(y(x) = ce^{2x} + \frac{5}{2}\)
Nous le démontrerons plus loin mais au cas où vous seriez hermétique aux démonstrations, dérivons la fonction de notre exemple pour que la formule ne vous paraisse pas tombée du ciel.
Prenons, par exemple, \(c = 4.\)
Donc \(y(x) = 4e^{2x} + \frac{5}{2}\)
D'après la formule, nous devons trouver \(y'(x) = 8e^{2x}.\)
Comme \(y'\) \(=\) \(ay + b\) alors \(y'(x)\) \(=\) \(2(4e^{2x} + \frac{5}{2}) - 5\)
\(y'(x) = 8e^{2x} + 5 - 5\)
\(\Leftrightarrow y'(x) = 8e^{2x}\)
Victoire !
Démonstration
La démonstration n'est pas exigible au programme de terminale. Mais elle peut satisfaire votre curiosité.
Soit l'équation \(y' = ay + b\)
En préambule, remarquons que la fonction constante \(y = -\frac{b}{a}\) est une solution particulière.
En effet, comme la fonction est constante, sa dérivée est nulle.
En outre, \(a × \frac{-b}{a} + b = 0\) également, donc on vérifie bien l'équation.
À présent, considérons deux fonctions \(f\) et \(g\) solutions de l'équation différentielle. On peut donc poser le système suivant :
\(\left\{ {\begin{array}{*{20}{c}}
{f' = af + b}\\
{g' = ag + b}
\end{array}} \right.\)
Par combinaison :
\(f' - g' = af - ag\)
Par propriété :
\((f - g)' = a(f - g)\)
Cette équation nous rappelle l'équation différentielle homogène \(y' = y\). Il s'ensuit que \((f - g)(x) = ce^{ax}\)
Donc \(f(x) = ce^{ax} + g(x).\) Ainsi, connaître \(g\) implique connaître \(f.\) Or, nous connaissons une fonction \(g\) est c'est \(g(x) = -\frac{b}{a}.\)
Par conséquent, \(f\) est du type \(f(x) = ce^{ax} - \frac{b}{a}\) et sa dérivée s'écrit donc \(f'(x) = ace^{ax}.\)
Or, quelle serait une expression de \(af + b\) ?
\(a(ce^{ax} - \frac{b}{a}) + b\)
Développons.
\(ace^{ax} - b + b = ace^{ax}\)
Eh oui, on trouve \(f'(x),\) ce qui signifie que l'on a bien vérifié l'équation \(y' = ay + b.\)
Exercices
1- Donner la solution générale de l'équation \(y' = 2y - 10\)
2-a. Donner une solution particulière de l'équation \(y' = 3y + 12\) et en déduire toutes les solutions.
b. Déterminer la solution de cette équation pour que la courbe représentative de la fonction \(y\) passe par le point de coordonnées \((0\, ; 4).\)
1- \(y' = 2y - 10\)
D'après la formule, \(y(x) = ce^{2x} + 5\) avec \(c ∈ \mathbb{R}.\)
2-\(y' = 3y + 12\)
a. Une solution particulière est celle d'une fonction constante. Elle est de la forme \(f'(x) = 3f(x) + 12\) avec \(f'(x) = 0.\) Donc \(f(x) = -4.\)
Les solutions de l'équation homogène \(y' = 3y\) sont de la forme \(y(x) = ce^{3x}\) avec \(c ∈ \mathbb{R}.\)
Donc les solutions s'écrivent \(y(x) = ce^{3x} - 4.\)
On retrouve évidemment ce résultat en appliquant directement la formule mais l'énoncé demandait un détail des étapes.
b. Il faut que \(y(0) = 4\)
\(ce^{0} - 4 = 4\) \(⇔ c = 8\)
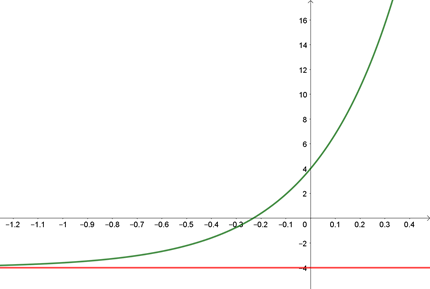
Donc \(y(x) = 8e^{3x} - 4\)
Pour information, la courbe représentative de \(y\) (en vert) et celle de la solution particulière (en rouge) :
L'étude des équations différentielles se poursuit avec celles qui sont du type \(y' = ay + f(x)\) (hors programme si vous avez opté pour maths complémentaires).
