Graphes non orientés au bac
L’exercice de spécialité de l’épreuve du bac ES de juin 2017 en Amérique du nord s’avère être un très bon exercice sur les graphes non orientés. Alors sans plus attendre, voici le sujet. Le corrigé suit mais bien sûr évitez de vous précipitez dessus.
Énoncé
- Sarah, une jeune étudiante en géologie, souhaite partir en voyage en Islande avec des amis. Elle a loué une voiture tout terrain pour pouvoir visiter les lieux remarquables qu’elle a sélectionnés.
- Sarah a construit le graphe ci-dessous dont les sommets représentent les lieux à visiter et les arêtes représentent les routes ou pistes :
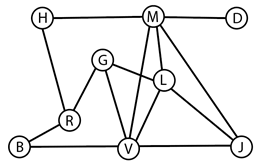
- B : le lagon bleu
D : chute d’eau de Dettifoss
G : geyser de Geysir
H : rocher Hvitserkur
J : lagune glacière de Jökulsárlon
L : massif du Landmannalaugar
M : lac de Mývatn
R : capitale Reykjavik
V : ville de Viko
- 1- Dans cette question, chaque réponse sera justifiée.
- a. Déterminer l’ordre du graphe.
b. Déterminer si le graphe est connexe.
c. Déterminer si le graphe est complet.
- 2- Sarah désire emprunter toutes les routes une et une seule fois. Déterminer, en justifiant, si cela est possible.
- 3- On appelle \(M\) la matrice associée au graphe précédent sachant que les sommets sont placés dans l’ordre alphabétique. On donne ci-dessous une partie de la matrice \(M\) ainsi que la matrice \(M^4\) :

- a. Il manque certains coefficients de la matrice \(M.\) Compléter et recopier uniquement la partie manquante de cette matrice.
b. Donner, en le justifiant, le nombre de chemins de longueur 4 permettant d’aller de B à D.
- 4. Sur le graphe pondéré ci-dessous, on a indiqué sur les arêtes les distances en kilomètres entre les différents lieux :
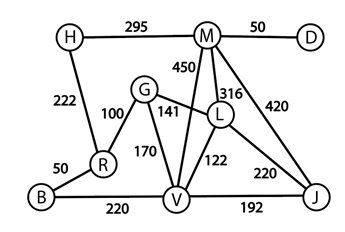
- Déterminer, à l’aide de l’algorithme de Dijkstra la distance minimale permettant d’aller du sommet B (lagon bleu) au sommet D (chute d’eau de Dettifoss). Préciser alors le trajet à emprunter.

Corrigé
1- a. Comme le nombre de sommets est 9, le graphe est d’ordre 9.
b. Le graphe est connexe parce qu’il existe un chemin qui passe par tous les sommets une fois et une seule. Exemples : H-R-B-V-G-L-J-M-D ou encore D-M-H-R-B-V-G-L-J…
c. Tous les sommets ne sont pas reliés par une arête. Exemple : R et V. Donc le graphe n’est pas complet.
2- Six sommets sont de degré impair (D, G, J, M, R et V). Le graphe n’admet donc pas de chaîne eulérienne et Sarah ne pourra pas emprunter toutes les routes une seule fois.
3-a. La matrice d’adjacence complétée :

On s’attache aux liens entre les sommets M, R et V avec les sommets B, D et G. On indique 0 quand il n’existe pas de lien et 1 quand il y en a un.
b. Le nombre de chemins de longueur 4 entre chaque sommet est donné par la matrice M4. On regarde l’intersection entre B et D (ou D et B), donc première ligne et deuxième colonne (ou deuxième ligne et troisième colonne). Nous lisons 3.
Ce sont : B-V-J-M-D, B-R-H-M-D et B-V-L-M-D.

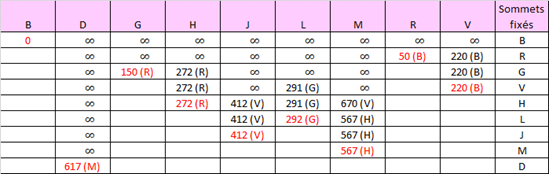
Le plus court chemin de B à D est B-R-H-M-D (partez de la fin pour le trouver, c’est plus facile), soit un trajet de 617 km.
