Exemples de matrices associées aux graphes
On trouve les matrices dans des applications particulièrement variées. Dame Nature a doté ces bestioles-là d’une telle faculté d’adaptation qu’elles prolifèrent dans les algorithmes de toute sorte.
À travers trois exemples, nous allons voir le lien qui existe entre graphes et matrices.
Construction
Des matrices d'adjacence aux graphes sont des matrices carrées dont chaque élément indique si tel sommet (en ligne) est relié à tel autre (en colonne).
S'ils ne le sont pas, le coefficient situé à la croisée des deux sommets est nul. Sinon, il est de 1 dans le cas d'un le graphe non pondéré et de la pondération s'il l'est.
La matrice d'adjacence d'un graphe non orienté est symétrique (exemple 1). Lorsque le graphe est orienté, les origines des arcs sont en ligne tandis que leurs extrémités sont en colonnes (exemples 2 et 3).
Exemple 1 : graphe non orienté
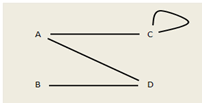
Il existe quatre sommets. On représente donc ce graphe par une matrice \(4 × 4.\)
Comme le graphe n’est pas orienté, la matrice est symétrique, c'est-à-dire que la diagonale agit comme un miroir entre le nord-est et le sud-ouest. Ainsi, le sommet \(A\) (1re ligne) est lié à \(C\) et à \(D\) (3ème et 4èmecolonne) et la réciproque est vraie aussi. Une liaison vaut 1 et une absence de liaison vaut 0. Une matrice qui n’est pas assez riche pour posséder autre chose que des 1 et des 0 est dite « booléenne ».
Pour être plus clair, écrivons la matrice associée :

Les lettres ne sont là que pour expliciter les liens. Nous nous en passerons désormais.
Exemple 2 : graphe orienté non pondéré
La puissance \(n\) d’une matrice est, comme vous vous en doutez, la multiplication d’une matrice par elle-même \(n\) fois. Nous allons voir que les chaînes de longueur \(n\) nous sont données par la matrice élevée à la puissance \(n.\)
Dans la mesure où un graphe est orienté, la matrice qui lui est associée est rarement symétrique.
Le graphe suivant représente les chemins qu’il est possible d’emprunter entre quatre maisons \(A,\) \(B,\) \(C\) et \(D.\) Les voies qui les relient sont pour la plupart à sens unique. Déterminons le nombre de parcours possibles entre deux maisons, puis trois, puis quatre.
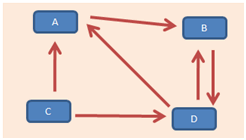
En lignes figurent les points de départ et en colonne les points d’arrivée.
\[\left( {\begin{array}{*{20}{c}} 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1\\ 1 & 0 & 0 & 1\\ 1 & 1 & 0 & 0\end{array}} \right)\]
Entre trois maisons : il suffit d’élever la matrice au carré.
\[\left( {\begin{array}{*{20}{c}} 0 & 0 & 0 & 1\\ 1 & 1 & 0 & 0\\ 1 & 2 & 0 & 0\\ 0 & 1 & 0 & 1\end{array}} \right)\]
Que signifie ceci ? Sur la première ligne, on ne relève qu’un 1 et c’est celui de la maison \(D.\) Il y a donc une chaîne de longueur 2 qui part de \(A\) et qui arrive à \(D\) (on voit que c’est \(A-B-D\)). Un 2 fait son apparition sur cette matrice. Il existe deux chaînes de longueur 2 qui partent de \(C\) et qui parviennent à \(B\) (\(C-A-B\) et \(C-D-B\)). Et ainsi de suite. Passons à la puissance 3 (chaînes entre quatre maisons). La matrice est encore différente (si l'on travaille dans l'algèbre de Boole, c'est-à-dire si l'on s'intéresse à l'existence des relations mais sans compter les chaînes par longueur, voir la fermeture transitive d'une relation binaire interne).
\[\left( {\begin{array}{*{20}{c}} 1 & 1 & 0 & 0\\ 0 & 1 & 0 & 1\\ 0 & 1 & 0 & 2\\ 1 & 1 & 0 & 1\end{array}} \right)\]
Avec une TI-83 : touche matrice, puis déplacement du curseur sur EDIT. Entrer. Saisie de la dimension de la matrice d’origine puis de ses valeurs. Touche matrice pour revenir au menu. Le curseur étant positionné sur le nom de la bonne matrice, entrer pour que seul le nom de la matrice figure sur l’écran (probablement [A]). Ensuite, x² pour une élévation au carré ou utilisation de la touche ^ (puissance).
Avec une Casio : voir les puissances d'une matrice.
Exemple 3 : graphe orienté pondéré
Dans d'autres problématiques, les arcs n'ont pas tous le même poids. Le graphe peut ne pas être orienté (voir l'exemple d'algorithme de Dijkstra où les arêtes sont pondérées par des distances entre des villes). Il peut aussi être orienté.
Lorsqu'il est orienté et pondéré par des probabilités, il est dit « probabiliste ». Il permet de visualiser un processus stochastique. Une matrice est dite stochastique lorsque tous ses coefficients sont positifs ou nuls et si la somme des coefficients de chaque ligne est égale à 1. Un exemple figure en page de graphes probabilistes (rappel des principes et extrait d'une épreuve de bac).
Pourquoi un graphe probabiliste ? L'intérêt pratique est celui d'étudier le passage d'un état à un autre dans un contexte d'incertitude. À partir d'un état initial, on simule ainsi des états successifs, éventuellement en se projetant sur l'infini. Par exemple, on extrapole les proportions de citadins et de ruraux en Europe sachant qu'il existe aussi bien un exode rural qu'un retour à la campagne. Si aucun facteur exogène ne vient gripper cette belle mécanique, les états vont évoluer de façon prévisible pour peut-être atteindre, à long terme des proportions stables. Voir les chaînes de Markov.
Pour effectuer les calculs, on recourt soit aux matrices soit aux suites. Après avoir reporté les probabilités dans une matrice carrée, on peut connaître l'état d'une évolution après \(n\) périodes. Il suffit d’élever la matrice de transition à la puissance \(n.\) Sous certaines conditions, après une certaine valeur de \(n,\) la matrice ne bouge plus.
Illustration : un panel de consommateurs est partagé en trois catégories en fonction d’une appétence pour un produit. On trouve de gros consommateurs (G), des occasionnels (O) et des réfractaires (R). Un an plus tard, on mesure leur probabilité d’appartenir à telle catégorie en fonction de leur profil en début de période. On obtient ce graphe et sa matrice de transition :
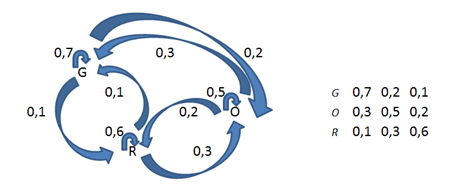
Élevons celle-ci à la puissance 5, ce qui permet d’estimer les modifications d’appétence des consommateurs quatre ans après l’état initial si l'on fait l'hypothèse que les probabilités restent les mêmes.
\[\left( {\begin{array}{*{20}{c}} 0,43 & 0,32 & 0,25\\ 0,41 & 0,32 & 0,27\\ 0,37 & 0,33 & 0,29 \end{array}} \right)\]

On peut s’amuser à « augmenter la puissance ». On remarque alors que cet état est stable puisque la matrice ne bouge plus. Il est ainsi possible d’établir des prévisions à moyen terme mais aussi de modifier légèrement l’état initial afin de savoir quel type de consommateur il est d'ores et déjà préférable de cibler par des campagnes publicitaires.
Voir aussi l'exercice sur graphe non orienté.
