Fermeture d'une relation binaire interne
Le contenu de cette page est très théorique mais il permet des prolongements pratiques. Sa lecture suppose une connaissance (même très légère) de l’algèbre de Boole, de la théorie des ensembles et des matrices. Elle vous dirigera ensuite vers les graphes orientés.
Opérations sur matrices booléennes
Soit \(a_{ij}\) l’élément de la ième ligne et de la jème colonne d’une matrice \(A\) de \(n\) lignes et \(p\) colonnes et \(b_{ij}\) l’élément ayant la même position dans une matrice \(B,\) de mêmes dimensions que \(A.\)
La somme de matrices ne pose pas de difficulté. Soit la matrice \(C = A + B.\)
Alors \(c_{ij} = a_{ij} + b_{ij}.\)
Il faut juste se souvenir que, comme nous évoluons dans l’algèbre de Boole, nous obéissons à cette inhabituelle égalité : \(1 + 1 = 1.\)
Exemple :
\(\left( {\begin{array}{*{20}{c}} 1&0\\ 1&0\end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0&0\\ 1&1\end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1&0\\ 1&1\end{array}} \right)\)
La multiplication est plus fastidieuse si on l’effectue manuellement. Certes, les règles de la multiplication sont en l’occurrence les mêmes qu’avec l’algèbre habituelle (\(0 \times 1 = 0...\)), mais une multiplication matricielle nécessite des additions puisque \(c_{ij}\) est obtenu en faisant la somme booléenne des produits des éléments de la ième ligne de \(A\) avec ceux, de même rang, de la jème colonne de \(B.\) Rappelons que si l’on multiplie \(A \times B,\) il faut que le nombre de colonnes de \(A\) soit égal au nombre de lignes de \(B.\)
\(\displaystyle{c_{ij} = \sum_{k=1}^p (a_{ik} \times b_{kj})}\)
Exemple :
Soit \(\displaystyle{A = \left( {\begin{array}{*{20}{c}} 1&0\\ 0&1\\ 1&1 \end{array}} \right)}\) et soit \(\displaystyle{B = \left( {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1 \end{array}} \right)}\)
\(\displaystyle{A \times B = \left( {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&1\\ 0&1&1 \end{array}} \right)}\)
Pour vos calculs en algèbre de Boole, vous pouvez vous rendre ici :
https://fr.symbolab.com/solver/boolean-algebra-calculator
Rappelons que la matrice identité est neutre pour la multiplication.
Union et composition de relations
Soit un ensemble \(E\) et deux relations \(R\) et \(S\) définies sur \(E.\) Les matrices \(A\) et \(B\) qui leur sont associées sont carrées puisque source et but sont identiques (le nombre d’éléments est donc le même).
L’union de \(R\) et de \(S\) est \(R \cup S.\) Sa pour matrice associée \(A + B.\)
Exemple :
Soit \(E = \{a, b, c\}\)
La relation \(R\) figure en haut et \(S\) en bas :
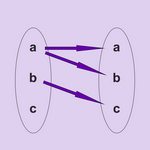
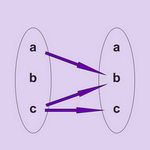
Soit la relation \(R \cup S\) :
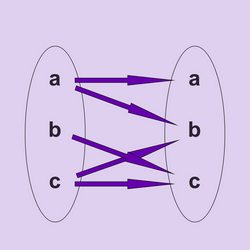
Graphiquement, ce sont les flèches de \(R\) plus celles de \(S.\) Une relation qui existe deux fois n’apparaît qu’une seule sur \(R \cup S,\) ce qui est cohérent avec l’algèbre de Boole dans laquelle \(1 + 1 = 1.\) D’ailleurs, les matrices associées à ces relations le vérifient :
\(\left( {\begin{array}{*{20}{c}} 1&1&0\\ 0&0&1\\ 0&0&0 \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&0\\ 0&1&1 \end{array}} \right)\) \(=\) \(\left( {\begin{array}{*{20}{c}} 1&1&0\\ 0&0&1\\ 0&1&1 \end{array}} \right)\)
La composition est une opération un peu plus délicate. Sur \(E,\) tout couple \((e_i, e_j)\) qui vérifie la relation composée \(S \circ R\) remplit les conditions suivantes : \((e_i, e_k)\) appartient au premier graphe \((R)\) et \((e_k, e_j)\) appartient au second \((S).\)
La matrice associée est la matrice produit \(A \times B.\)
Exemple. Reprenons nos relations ci-dessus.
- La relation \(R\) montre que \(a\) « va vers » \(a\) et \(b.\) Puis \(S\) montre que \(a\) a pour but \(b\) lequel n'est source d'aucune relation. Donc dans la relation composée \(a\) ne se dirige que vers \(b.\)
- \(R\) montre que \(b\) va vers \(c\) puis \(S\) montre que \(c\) va vers \(b\) et \(c.\) Donc \(b\) se dirige vers \(b\) et \(c\) dans la relation composée.
- Comme aucune relation n'a \(c\) pour origine dans \(R,\) c’est la même chose dans la composée.
Avec les matrices :
\(\left( {\begin{array}{*{20}{c}} 1&1&0\\ 0&0&1\\ 0&0&0 \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} 0&1&0\\ 0&0&0\\ 0&1&1 \end{array}} \right)\) \(=\) \(\left( {\begin{array}{*{20}{c}} 0&1&0\\ 0&1&1\\ 0&0&0 \end{array}} \right)\)
Nous retrouvons bien nos résultats.
Pour ce type d'exercice, vos calculs sont vérifiables sur le web (voir adresse plus haut) ou sur calculatrice mais en remplaçant tous les nombres différents de zéro par 1 (les calculatrices n’ayant pas d’option « algèbre de Boole »).
Fermeture transitive
Notations : \(R^0\) est associée à la matrice identité et \(R^1 = R.\)
\(R^2 = R \circ R\)
\(R^3 = R \circ R^2\)
\(R^{n+1} = R \circ R^n\)
La fermeture transitive faible de \(R\) est la relation \(R^1 \cup R^2 … \cup R^n\) et sa fermeture transitive forte est \(R^0 \cup R^1 \cup R^2… \cup R^n.\)
Important : il existe toujours une valeur de \(n\) finie pour vérifier une fermeture forte. En d’autres termes, pas besoin d’effectuer une infinité de multiplications d’une matrice booléenne par elle-même pour qu’elle se stabilise à une configuration qui ne changera plus. En guise d'exemple, voir les classes de connexité.
Note : dès lors qu’une relation a tous ses éléments bouclés (sa matrice associée comporte des 1 sur toute sa diagonale), elle est dite réflexive.
Il s’en suit que, si l’on nomme \(\hat{M}\) la matrice associée à la fermeture transitive de \(R,\) il existe un entier naturel \(n\) tel que \(\hat{M} = (I + M)^n.\)
