Première approche sur les suites
Cette page est destinée aux élèves de première (première générale et premières technologiques) qui découvrent la notion de suite. Et plus particulièrement ceux qui s’en trouvent fort perplexes et qui aimeraient bien comprendre un peu mieux cette curiosité…
Le principe
En fait, les suites n’ont rien de très curieux. Chacun peut s’imaginer une progression de nombres sans savoir que ça s'appelle ainsi. Par exemple, « 2, 4, 6, 8, 10 » est une suite.
Une suite est une fonction, souvent notée \(u,\) dont l'ensemble de définition est l’ensemble des entiers naturels \(\mathbb{N}\) ou une partie de celui-ci. Les valeurs prises par une suite sont le plus souvent des réels. Pour reprendre notre exemple, on pourrait noter \(u_1\) le premier terme qui est 2, le deuxième terme \(u_2\) étant 4, etc. Encore que le premier terme est très souvent nommé \(u_0.\) Comme vous êtes perspicace, vous avez deviné que notre exemple est la suite des cinq premiers nombres pairs.
Contrairement aux valeurs prises par une fonction continue, souvent notées \(f(x),\) le terme général de la suite n'est pas noté \(u(n)\) (sauf en premières technologiques !) mais \(u_n\) et le nom de la suite \((u_n)\) est toujours écrit entre parenthèses.
\(n\) est donc une sorte de compteur qu’il ne faut pas confondre avec la valeur prise par \(u_n.\) En l'occurrence, \(u_1,\) c’est-à-dire le terme numéro 1, est égal à 2. Vous comprenez au passage pourquoi \(n\) ne peut être qu’un entier naturel. Il serait bizarre de déterminer le « 1,6e terme » d’une suite !
Ce qui est embêtant, c’est que selon les exercices, le premier terme peut être le numéro 1 ou le numéro 0. Si vous n’êtes pas assez méfiant, vous risquez de tomber un jour dans un piège tendu par un prof perfide...
Deux modes de génération
Il existe des tas de sortes de suites mais en classe de première on ne s’intéresse qu’à celles qui possèdent une structure simple. Celle-ci peut être présentée de deux façons :
- soit avec une formule explicite (comme toute fonction mais \(n\) remplace \(x\)), par exemple \(u_n = n^2 + 1.\)
- soit par une relation de récurrence qui définit un terme par rapport au terme précédent, par exemple \(u_{n + 1} = u_n + 3.\)
La première est indispensable pour calculer un terme d’un rang élevé : si l’on cherche le centième terme, il est inutile de calculer les 99 précédents alors qu’avec la seconde méthode, on n’y coupe pas ! Par ailleurs, pour la deuxième présentation il faut TOUJOURS préciser quelle est la première valeur de la suite (sinon il est impossible de déterminer les autres valeurs).
La relation de récurrence offre l'occasion de réaliser des algorithmes avec des boucles (chic !).
Voir la page d'exercices sur les modes de génération.
Étude de suites
Pour étudier les suites, il est très important de garder à l’esprit ces deux techniques et d’employer celle qui convient en fonction de l'énoncé. Pour les illustrer, reprenons notre suite de nombres pairs. Si elle est définie par une formule explicite, on écrira \(u_n = 2n.\) Ainsi, le numéro du compteur permet de connaître directement le résultat : le premier terme \(u_1\) est \(2 \times 1 = 2,\) le deuxième terme est \(u_2 = 2 \times 2 = 4\) et ainsi de suite (c’est le cas de le dire).
Avec une formule de récurrence, il faut d’abord préciser \(u_1 = 2\) puis \(u_{n+1} = u_n + 2\) puisqu’on ajoute 2 à chaque fois. Remarquez la différence d’écriture : \(u_{n + 1}\) (avec +1 en indice) signifie qu’il s’agit du terme qui suit le terme \(u_n.\) Donc \(n + 1\) est un NUMÉRO. En revanche, \(u_n + 2\) (avec + 2 « en grand ») indique qu’il faut ajouter 2 à la VALEUR précédente. Avec l’habitude, cette distinction devient évidente mais lorsqu’on découvre les suites, c’est parfois déroutant.
Un sujet d’étude est le sens de variation des suites. Ces dernières peuvent être monotones ou non. Lorsqu’elles le sont, elles sont soit croissantes, soit décroissantes, soit constantes. Notre suite de nombres pairs est évidemment croissante puisque les valeurs qu’elle prend sont de plus en plus grandes. Si l’on définit une suite croissante de façon formelle, on a \(u_{n + 1} > u_n\) et le contraire pour une suite décroissante. Évidemment, si \(u_{n + 1} = u_n\) la suite est constante mais vous n’en rencontrerez pas souvent !

Un autre sujet est celui de la convergence (ce terme n'est pas au programme de première). Lorsque le rang augmente indéfiniment, la valeur des termes augmente-t-elle aussi indéfiniment ou ne dépasse-t-elle pas une valeur en particulier ?
Deux types de suites figurent au programme de première. Les suites arithmétiques sont celles où il faut AJOUTER toujours le même nombre à un terme pour obtenir le suivant (si ce nombre est positif, la suite est croissante et s’il est négatif elle est décroissante) et les suites géométriques sont celles où l'on MULTIPLIE chaque terme par la même valeur pour obtenir le suivant. Que la suite soit arithmétique ou géométrique, le nombre qui permet de passer d’un terme à un autre s’appelle la raison. La suite des nombres pairs que nous avons définie plus haut est une suite arithmétique.
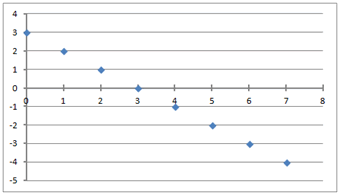
Graphiquement, une suite peut être représentée par des points. Prenons d’abord un exemple de suite arithmétique, définie sur \(\mathbb{N}\) par une formule explicite \(u_n = 3 - n,\) ou ce qui revient au même par la relation de récurrence, \(u_{n+ 1 } = u_n - 1\) avec \(u_0 = 3.\) Les points sont alignés de façon rectiligne parce que la suite est arithmétique et la droite qui pourrait les relier descend parce que cette suite est décroissante (la raison est -1, c’est un nombre négatif). La suite arithmétique est un modèle de croissance linéaire.
Vous trouverez en page de suite arithmétique de petits exercices adaptés à la filière générale. En première technologique, on se dirigera plutôt vers les suites arithmétiques avec Excel. Pour toutes filières, voir aussi le mode d'emploi des suites arithmétiques avec calculatrices TI et Casio.
Soit maintenant une suite géométrique définie sur \(\mathbb{N}\) par la formule explicite \(u_n = 2n\) ou ce qui est équivalent par la formule de récurrence \(u_{n +1} = 2u_n,\) le premier terme étant \(u_0 = 1.\) Vous l’avez deviné, la raison est 2.
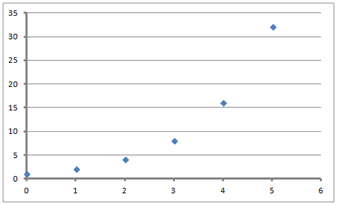
Cette fois-ci, les points ne sont pas alignés de façon rectiligne mais de façon exponentielle (ils décrivent une courbe qui monte de plus en plus verticalement).
On constate que la suite est croissante. En effet, le premier terme est positif et la raison est strictement supérieure à 1. Si elle avait été comprise entre 0 et 1 (exclus) ou si le premier terme avait été négatif, elle aurait été décroissante. Si la raison est 1, la suite géométrique ne présente aucun intérêt puisqu’en multipliant chaque fois par 1, on fait du sur-place (suite constante). De même si la raison ou si un terme est nul, tous les termes da la suite géométrique sont nuls. Enfin, si la raison est négative, la suite ne peut être ni croissante ni décroissante puisqu’il y a changement de signe en passant de \(n\) à \(n + 1.\) La raison -1 se traduit par une simple alternance entre un nombre et son opposé puisqu’une multiplication par -1 équivaut à changer de signe.
Vous pouvez vous amuser à créer des graphiques comme ceux-ci avec Excel. Les tableurs sont des outils idéaux pour travailler sur les suites et il est habituel de profiter de ce chapitre pour les utiliser en classe (particulièrement dans les filières technologiques).
