Initiation aux limites de suites avec Excel
En classe de première générale, les limites de suites sont au programme de maths mais sans vraiment en faire partie puisqu'il mentionne « une introduction intuitive de la notion de limite ». D’où un certain flottement qui se traduit par des cours non seulement assez différents d’un enseignant à l’autre mais aussi en fonction des manuels ! Cette page s'adresse aussi aux élèves de terminale générale pour rafraîchissement de mémoire.
Convergence
Précision : les termes de convergence et de divergence ne figurent qu'au programme de terminale (maths de spécialité).
Une suite est convergente si, à partir d’un certain rang, tous ses termes se rapprochent d’une valeur réelle. Sinon, elle est divergente.
Prenons un exemple simple. Soit une suite \((u_n)\) définie par \(u_0 = 0\) et \(u_{n+1} = u_n + 4\) pour tout \(n \in \mathbb{N}.\) C’est une suite arithmétique et vous avez deviné qu’elle est croissante. Si \(n\) est infiniment grand, alors le énième terme est infiniment grand lui aussi. Il s'ensuit que cette suite est divergente.
Autre exemple, lui aussi de compréhension facile. La suite \((v_n)\) est définie, pour tout \(n > 0,\) par \(v_n = \frac{1}{n}.\) Son comportement est bien sûr le même que celui de la fonction inverse, c’est-à-dire que plus \(n\) est grand, plus les termes se rapprochent de zéro. Et pourtant, aucun d’entre eux ne peut être tout à fait nul. Cette suite converge vers 0.
Tableur
Il est très simple de visualiser cette suite avec Excel ou tout autre tableur. Contentons-nous des douze premières valeurs. D’abord, déterminons-les :
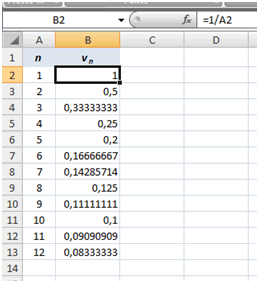
La première valeur est calculée avec =1/A2 qui apparaît dans la barre de formule ; elle est recopiée sur les onze lignes suivantes.
Ensuite, il faut tout sélectionner et opter pour Insertion dans le ruban puis, dans le choix de graphiques, cliquer sur Nuage de points. Afin d'être plus esthétique que la présentation par défaut, l’illustration ci-dessous a bénéficié de quelques modifications « cosmétiques ».
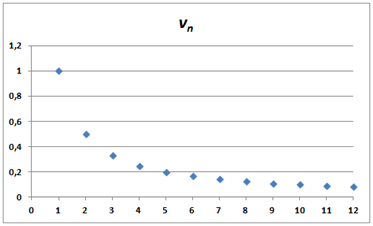
Dès lors, on conjecture que les termes se stabiliseront aux alentours de 0. La suite est probablement convergente.
Remarques : indications pour l’amélioration esthétique du graphe. Clic droit sur l’un des points puis choisir Mettre en forme une série de données… Les options de marqueur permettent de modifier la taille et la forme des points, le remplissage des marqueurs permet de changer leur couleur, etc. Clic droit sur chacun des axes pour modifier le pas, les valeurs extrêmes, la police de caractère…

Exercice
\((u_n)\) est définie pour tout \(n \in \mathbb{N}\) par \(u_n = n^2 - 3n + 1.\) Déterminer les 16 premiers termes de cette suite et les représenter graphiquement. \((u_n)\) semble-t-elle convergente ?
Corrigé
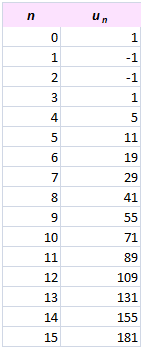
Remarque : les seize premiers termes comprennent le rang 0 ; le dernier point à représenter est donc de rang 15.
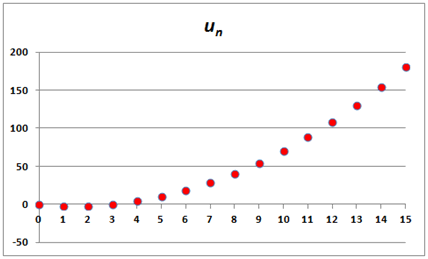
Cette suite est très probablement divergente (si l’on prolongeait indéfiniment la série de points, on constaterait qu'elle ne plafonne jamais).
On le prouve très facilement en étudiant la fonction \(f\) défine par \(f(x) = x^2 - 3x + 1.\)
Voir aussi les suites géométriques.
