Fonction \(a^x\) et calculs avec puissances
Voici une fonction usuelle, abordée en terminale et au cours des études supérieures. C’est la fonction de type \(a^x,\) \(a\) étant un réel strictement positif. Si vous êtes en classe de terminale, dirigez-vous plutôt en page d'introduction à aux fonctions exponentielles, rédigée pour vous.

La fonction
Mise en garde : il serait malvenu de confondre cette fonction avec une fonction puissance, de type \(x^a.\)
On établit ainsi le lien avec la fonction exponentielle de base \(e\) : \(a^x=e^{x\ln a}\)
L'ensemble de définition est particulièrement vaste puisqu’il s’agit de \(\mathbb{R}.\) L’exigence de stricte positivité ne porte que sur \(a\) et l’égalité ci-dessus permet de comprendre pourquoi (condition d’existence d’un logarithme).
Donc, à l’instar de la fonction exponentielle de base \(e,\) celle de n’importe quelle base strictement positive est continue, convexe, strictement positive et monotone.
Cette monotonie se traduit par une croissance si \(a\) est strictement supérieur à 1 et par une décroissance si \(a\) est compris dans l’intervalle \(]0\,; 1[.\) Il est bien évident que si \(a = 1,\) la fonction est constante…
Il est tout aussi évident que, quel que soit \(a,\) la courbe représentative de la fonction passe par le point de coordonnées \((0\,; 1)\) et que ladite fonction prend la valeur \(a\) lorsque \(x\) est égal à 1.
La dérivée est \(f’(x) = (\ln a)a^x.\) Là encore, la formule ci-dessus permet de la retrouver facilement.
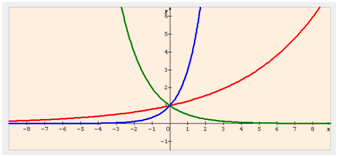
Ci-dessous, la courbe bleue représentative de la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x) = 3^x\) donne tout son sens à l’expression croissance exponentielle. La courbe rouge représente une fonction d'équation \(g(x) = 1,25^x.\) La verte illustre \(h(x) = 0,5^x\) (réalisation avec SineQuaNon).
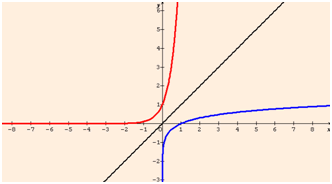
Dans la mesure où il s’agit d’une application bijective (fonction monotone continue), la fonction exponentielle de base \(a\) admet une réciproque. Il s’agit de la fonction logarithme de base \(a.\) Ainsi, la réciproque de la fonction définie par \(f(x) = 10^x\) est la fonction logarithme décimal (représentation des deux fonctions ci-dessous).
Les primitives de la fonction sont de la forme suivante (la lettre \(c\) indiquant une constante) :
\(F(x) = \frac{a^x}{\ln a} + c\)
La fonction exponentielle de base \(a\) est rarement rencontrée telle quelle, en particulier dans les exercices de maths. Dans les situations les plus simples, il existe au moins un réel \(b\) qui vient jouer les trublions en multipliant notre \(a^x\) et la fonction prend la forme \(f(x) = ba^x.\) C’est ainsi que l’on retrouve la version « continue » (de \(\mathbb{R}\) dans \(\mathbb{R}\)) d’une suite géométrique (de \(\mathbb{N}\) dans \(\mathbb{R}\)) qui s’exprime quant à elle sous la forme \(u_n = u_0 \times q^n,\) \(q\) étant la raison. Dans les applications économiques, la suite géométrique se rencontre beaucoup plus souvent que la fonction exponentielle de base \(a.\)
Propriétés
Cette page est l’occasion de rappeler les règles de calcul sur les puissances (règles valables même si \(a\) est négatif) :
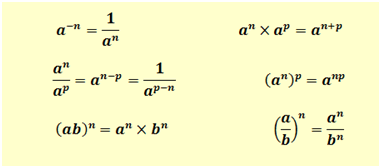
Rappelons qu'une racine énième équivaut à une puissance \(\frac{1}{n}.\)
Résolution d’équations :
\(x^{\frac{n}{p}} = a^m \Rightarrow x = a^{\frac{mp}{n}}\)
Exercice
Un entraînement au passage d’une puissance à l’exponentielle d’un logarithme...
Pour tout \(x\) strictement positif, déterminer la dérivée seconde de la fonction définie par \(f(x) = x^x.\)
Corrigé détaillé
Notre petite transformation, très pratique, nous permet d’écrire \(f(x) = e^{x \ln x}\)
On recourt à deux formules de dérivées pour exprimer \(f’(x).\) On sait que la dérivée de \(e^{u(x)}\) est de la forme \(u'(x)e^{u(x)}\) mais pour trouver \(u’(x)\) il faut remarquer que \(x \ln x\) se présente sous la forme d'un produit de fonctions \(v(x) \times w(x)\) dont la dérivée s'écrit \(v’(x)w(x) + w’(x)v(x).\)
\(u'(x) = \ln x + x(\frac{1}{x}) = \ln x + 1\)
Ainsi \(f’(x) = (\ln x + 1) e^{x \ln x},\) donc \(f’(x) = (\ln x + 1)x^x.\)
Dérivons ce beau résultat pour obtenir la dérivée seconde. Encore un produit de fonctions.
\(f''(x) = \frac{1}{x} \times e^{x \ln x} + (\ln x + 1)[x^x(\ln(x + 1))]\)
En factorisant par \(x^x,\) alias \(e^{x \ln x},\) il s’ensuit ...
\(f''(x) = x^x\left[\frac{1}{x} + (\ln x + 1)^2 \right]\)
Note : le calcul de la limite en 0 de cette fonction figure en page exercices sur limites avec exponentielles.
