Fonctions carré et de puissance \(n\)
Quelques rappels sur les puissances entières…
La puissance
Pour tout réel \(x\) et pour tout entier \(n\), \(x\) à la puissance \(n\) équivaut à écrire \(x \times x \times x...\) (\(n\) fois). L’expression se note \({x^n}\). Une fonction monôme est une fonction de puissance entière éventuellement multipliée par un coefficient.
La puissance zéro
Quel que soit le réel \(x\), \(x\) à la puissance zéro est égal à 1. La fonction puissance 0 est donc constante.
La puissance 1
Quel que soit le réel \(x\), \({x^1} = x\). La fonction puissance 1 est donc linéaire.
La fonction carré
Chacun sait ce qu’est un carré (oui, la figure géométrique). Si son côté mesure \(x\), sa surface s’établit à \({x^2}\). Le nom de « carré » a été consacré pour définir la puissance 2.
Un carré est toujours positif ou nul. En effet, le produit de deux nombres de même signe est positif et il en est bien sûr de même lorsqu'on multiplie un nombre par lui-même. Propriété qui se vérifie d'ailleurs pour toute puissance paire. En revanche, \({0^2} = 0\), comme n’importe quelle puissance de 0.
La fonction carré \(x \mapsto {x^2}\) définie sur \(\mathbb{R}\) montre donc pour chaque image deux antécédents (sauf 0 qui n'en a qu'un). Ainsi, 4 est aussi bien le carré de 2 que de -2. Avis aux lecteurs qui sont en classe de seconde : la suite de cette page sera hors programme et vous êtes invité à bifurquer en page fonctions de référence, puis tableau de variation, où la fonction carré est brièvement présentée.
Bref, cette fonction usuelle, définie pour tout réel, est paire, continue, convexe et dérivable partout. Sa dérivée, égale à \(2x\), s’annule en 0.
En \( - \infty \) comme en \( + \infty \), ses limites sont \( + \infty \).
La représentation graphique est bien connue. C’est une parabole (réalisation SineQuaNon).
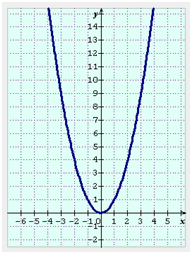
Sur \(\mathbb{R}_+\), la fonction carré a pour réciproque la fonction racine carrée (en rouge) :
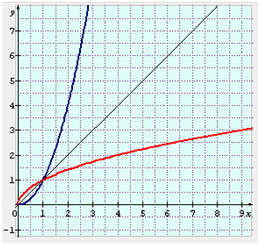
Une fonction carré multipliée par un réel conserve les mêmes caractéristiques. Par exemple, la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x) = 3{x^2}\) est elle aussi paire, continue, dérivable et ses limites à l’infini sont les mêmes que pour \({x^2}\). Sa courbe représentative est plus serrée que celle de sa fonction de référence et si l’on multiplie la fonction carré par un nombre compris entre 0 et 1, la parabole est au contraire plus évasée. Multipliée par un nombre négatif, elle est concave (tournée vers le haut) et située en territoire négatif. Ajoutée à une fonction affine, elle devient une fonction trinôme et conserve là encore une partie des caractéristiques de la fonction carré.
La fonction cube (ou cubique)
Le volume d’un cube est égal à son côté multiplié trois fois par lui-même. On a consacré ce terme de « cube » pour nommer la puissance 3.
Un cube n’est pas toujours positif. Un nombre négatif élevé à une puissance impaire est en effet négatif. Ainsi, la fonction cube n’a pas les mêmes caractéristiques qu’une fonction carré : définie, continue et dérivable partout, elle est impaire et sa dérivée est égale à \(3{x^2}\). Elle partage deux points avec elle : l’origine et le point de coordonnées \((1\,;1)\) qui d'ailleurs est commun à TOUTES les puissances, zéro compris. Sa dérivée s’annule elle-aussi en 0 mais il s'agit d'un point d'inflexion et non d'un extremum.
Voir une présentation destinée aux élèves de seconde en page fonctions de référence et de première générale, avec la courbe représentative, en page de fonction cube.
Croissante, sa limite en \( - \infty \) est \( - \infty \) et elle s’envole à \( + \infty \) lorsque \(x\) tend vers \( + \infty \).

Les puissances supérieures à 3
Les caractéristiques des puissances paires sont les mêmes que celles de la fonction carré et celles des puissances impaires sont les mêmes que celle de la fonction cube.
Graphiquement, plus les puissances sont élevées, plus les courbes sont resserrées et plus elles montrent une courbure forte entre -1 et 1. La fonction carré est représentée en bleu, la cube en vert, la puissance 4 en rouge et la puissance 5 en marron.
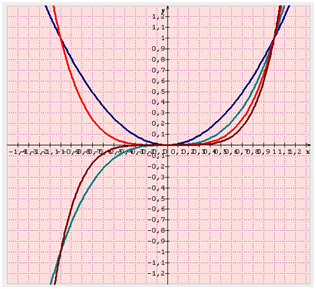
Pour aller plus loin : il existe aussi des fonctions de puissances non entières (voir les fonctions puissances).
