Points et coordonnées
En mathématiques, le point est une notion essentielle et pas seulement en géométrie. Mais quelle est cette chose qui semble si simple mais qui s’avère si étrange ?
Historique
Le point apparaît en Grèce, plus précisément avec Euclide qui en donne deux définitions (l’indivisibilité et les extrémités d’une ligne), ce qui alimenta des controverses mathématiques durant deux millénaires. Aujourd’hui encore, il n’en existe pas de définition unique.

Le terme vient du latin punctus qui signifie « piqûre ».
Il est si petit…
Un point est un objet mathématique infiniment petit. Il n’y a d’ailleurs rien de plus petit qu’un point au sens mathématique. En effet, un nombre infiniment petit peut toujours être divisé par deux alors que la notion de demi-point n’existe pas !
La définition du point peut être étendue. Le cas du nuage de points, en statistiques, est un peu particulier. dans une image numérique, un pixel est considéré comme un point : c’est le plus petit élément existant. Préfiguré par les peintures pointillistes de la fin du dix-neuvième siècle (comme Seurat, ci-dessous), il n’est pas pour autant infiniment petit.

Où le trouver ?
En géométrie, une droite ou une figure géométrique (triangle, quadrilatère…) est un ensemble de points. En analyse, une courbe représentative d’une fonction est aussi un ensemble de points. Ces ensembles sont infinis puisque, un point étant infiniment petit, il s'en trouve une infinité dans un segment, quelle que soit la taille de celui-ci.
Évidemment, par convention, on le représente de façon qu’il soit visible ! Généralement, c’est avec une petite croix ou un petit disque.
Les points intéressants sont nommés avec une lettre majuscule. En géométrie, il s’agit des lieux remarquables (extrémités d’angles, centres de cercles…) tandis qu’en analyse ils marquent les retournements de courbes ou les points d’inflexion, par exemple. Dans tous les cas, ils indiquent aussi les intersections et les lieux de tangence (voir par exemple les pages sur les tangentes en analyse et sur la tangente à un cercle).
Existe-t-il aussi des points à l’infini ? Oui, bien sûr. Vous ne les trouverez pas en branchant un microscope électronique sur un télescope car cette notion est encore plus théorique ! Par exemple, on considère que deux droites parallèles se croisent à l’infini ; il existe donc un point d’intersection à l’infini.
Coordonnées
En géométrie pure, un point n’existe que par rapport à d’autres. Un rectangle de dimensions données existe dans l’absolu. En géométrie analytique et en analyse, il est placé dans un repère.
Un repère peut n’avoir qu’une dimension. C’est la droite numérique. Un point de cette droite représente un nombre. Il y a une infinité de points puisqu’il y a une infinité de réels.
Lorsqu’un repère définit deux dimensions, le point s’inscrit dans un plan. On a besoin de deux coordonnées pour le situer. Par convention, la première est l’abscisse la seconde l’ordonnée.
Lorsque le repère est orthogonal, l’axe horizontal est celui des abscisses (nommées \(x\)) et l’axe vertical celui des ordonnées (nommées \(y\)). Un point \(A\) ayant pour abscisse 2 et pour ordonnée 4 se note \(A(2\, ;4).\) Ne pas ajouter le symbole \(=.\) Illustration avec GeoGebra...
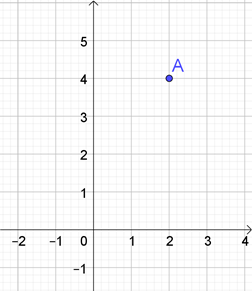
Il s’agit là de coordonnées cartésiennes. Un point peut aussi être défini par des coordonnées polaires (la longueur d’un vecteur par rapport à l’origine et l’angle qu’il forme par rapport à l’axe des abscisses).
Une surface non plane permet aussi de situer des points, quitte à utiliser d’autres notions que les abscisses et les ordonnées. Par exemple, un point de la surface terrestre est défini par une latitude (parallèle à l’équateur) et une longitude. Voir la page sur le repérage.
Dans un espace à trois dimensions, on a besoin de trois coordonnées. Le troisième axe est celui des cotes (nommées \(z\)). Un solide est aussi un ensemble infini de points.
Il n’est pas possible de représenter un espace ayant davantage de dimensions mais là aussi, les points s’y trouvent très bien…
Geogebra
Exposons deux façons de placer un point dans un plan repéré avec Geogebra.
- On clique sur le bouton représentant un point \(A\) puis à son emplacement sur le plan. Si la définition des coordonnées est simple (ce sont par exemple des entiers), c’est la technique la plus rapide puisque si l’on clique légèrement à côté de coordonnées entières le point est « aimanté » là où l’on aurait probablement voulu le placer.
- On entre les coordonnées dans la barre de saisie mais contrairement à l’écriture habituelle il faut indiquer le symbole \(=\) et séparer les coordonnées avec une virgule et non un point-virgule.
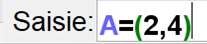
Cette technique permet des saisies précises.

