Initiation aux vecteurs
Cette page est une initiation aux vecteurs. Elle reprend une partie du chapitre qui leur est consacré dans le programme de seconde (à compléter par les vecteurs et coordonnées). Pour qui souhaite poursuivre ses études en filière scientifique ou retrouver après bac un cursus contenent un solide programme de maths, c'est le début d'une longue et enrichissante épopée mathématique.
Translation
En classe de seconde, on présente un vecteur comme une translation géométrique, donc une projection d’un point ou d’une figure dans le plan (pour la géométrie vectorielle dans l'espace, il faut attendre la terminale).

Une translation est définie par trois critères : une longueur (distance), un sens et une direction. Dans le plan, on la représente par une flèche. C'est un vecteur. S’il n’y avait qu’une DIRECTION infinie, ce serait une droite ou une demi-droite. Si cette direction était finie (donc, avec une LONGUEUR), ce serait un segment de droite. Mais la flèche indique aussi un SENS (selon que sa pointe est d'un côté ou de l'autre).
Ainsi, une translation qui transforme un point \(A\) en un point \(B\) associe n’importe quel point \(C\) à un unique point \(D.\) Un vecteur n’est pas positionné à un lieu précis du plan, même si c’est bien à partir d’un endroit particulier qu’on va souvent le définir. Le vecteur lui-même peut être translaté. Illustration ci-dessous avec WxGéométrie (devenu Géophar) :
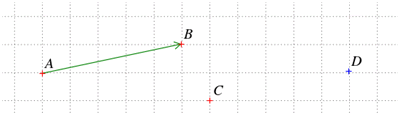
Le vecteur qui a pour origine \(A\) et pour extrémité \(B\) est le même que celui qui partirait de \(C\) pour aller à \(D.\) On écrit : \(\overrightarrow {AB} = \overrightarrow {CD}. \)
Définissons ce vecteur comme un trajet de cinq carreaux sur la droite et d’un carreau vers le haut. Tout vecteur ainsi décrit ainsi est le représentant du vecteur qui transforme \(A\) en \(B.\) Ceci nous amène à la règle du parallélogramme : l’égalité ci-dessus se vérifie si et seulement si \(ABDC\) est un parallélogramme (attention à l’ordre des points).
Un vecteur qui transforme un point en lui-même est le vecteur nul. Il n’a ni sens ni direction. Ainsi, pour tout point \(A\) on a \(\overrightarrow {AA} = \overrightarrow 0 \)
Deux vecteurs s’additionnent. Si le point d’arrivée de l’un est le même que le point de départ de l’autre, on obtient la relation de Chasles :
\[\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} = \overrightarrow {AD} \]
Un exercice simple, de niveau seconde, est donné en page de relation de Chasles (cette page montre aussi que cette fameuse relation s’applique à d’autres domaines que les vecteurs mais vous ne verrez ceci qu’en première générale ou en terminale). Voir aussi le théorème de Varignon.
Cela étant, comme l’emplacement des vecteurs n’a pas d’importance, nul besoin que ceux-ci se suivent pour s’additionner (exercice 1 ci-dessous).
Un vecteur opposé à un autre a la même longueur et la même direction mais, graphiquement, la flèche est orientée dans l’autre sens. En effet, le point de départ de l’un est l’image de l’autre et inversement. Donc : \(\overrightarrow {AB} = - \overrightarrow {BA}. \)
Chaque fois que vous trouverez une soustraction dans vos exercices, nous vous conseillons de les remplacer par des additions dès la première étape de calcul.
En outre, les vecteurs permettent de caractériser un milieu. Le point \(M\) est le milieu du segment \([AB]\) si \(\overrightarrow {AM} = \overrightarrow {MB} .\)
Enfin, on peut multiplier un vecteur par un réel. Si celui-ci est positif, sa longueur est ainsi multipliée. S'il est négatif, le sens change.
Les vecteurs permettent de démontrer des égalités et des propriétés (exercice 2 ci-dessous).
Exercices
Exercice 1. Soit un rectangle \(ABDC,\) les milieux de ses côtés étant les points \(E,\) \(F,\) \(G\) et \(H\) et \(I,\) milieu du rectangle. Maintenant que les présentations sont faites, complétez les égalités :
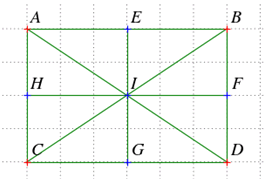
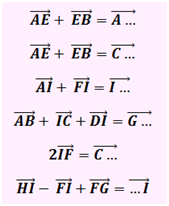
Exercice 2. Soit un triangle \(ABC\) et \(M\) le milieu de \([AB].\) Soit \(D\) l’image de \(B\) par translation de \(C\) en \(A.\) Démontrer que \(M\) est le milieu de \([CD],\) au besoin en s’aidant d’une figure.
Corrigés
Exercice 1

Exercice 2
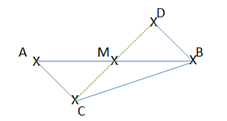
Si l’on traduit l’énoncé en langage plus clair, nous avons \(\overrightarrow {BD} = \overrightarrow {CA} .\)
On en déduit que \(CADB\) est un parallélogramme (d’après la bien nommée règle du parallélogramme). Donc le milieu de \([AB]\) est aussi le milieu de \([CD]\) (voir la page géométrie analytique si par malheur vous aviez oublié ce détail). Comme c’est \(M\) qui est le milieu de \([AB],\) \(M\) est bien le milieu de \([CD.]\)
