Droites et segments
-
La ligne géométrique est un être invisible. Elle est la trace du point en mouvement, donc son produit. Elle est née du mouvement, et cela en premier lieu par l'anéantissement de l'immobilité suprême du point. Ici se produit alors le bond du statique vers le dynamique (V. Kandinsky, Point et ligne sur plan, 1926). Ci-dessous,
Horizontalée de Kandinsky (1974), musée d'Art moderne de Paris.

A priori, rien de moins intéressant qu’une droite. Un trait infini, abstrait, tout bête, ni beau ni laid, connu de tous depuis le CE2… Écrire là-dessus, c’est comme écrire sur l’ensemble vide, c’est blablater sur pas grand-chose. Mais bon, dans sa course à l’infini, ce machin doit bien faire une rencontre intéressante à un moment donné alors étudions-le de plus près…
Note : si vous êtes en classe de seconde ou de première, voyez plutôt la droite dans le plan.
Définitions et géométrie pure
Soit deux points \(A\) et \(B.\) Une droite \((AB)\) est l'ensemble des points qui sont alignés avec \(A\) et \(B.\)
Si la droite est limitée d’un côté, on parle de demi-droite. Si cette limite est en \(A,\) elle est notée \([AB).\) Des deux côtés, c’est un segment de droite, noté \([AB].\)
Deux droites sont sécantes si elles se croisent et parallèles dans le cas contraire. Deux droites qui se coupent à angle droit sont perpendiculaires. Toutes les droites sécantes en un même point forment une famille.
Lorsque deux droites sont sécantes, leur intersection est un point.
Si dans le plan deux droites sont soit sécantes soit parallèles, elles peuvent n’être ni l’un ni l’autre dans l’espace.
L’orthogonalité est une notion plus large que la perpendicularité puisqu’il n’est pas nécessaire que les droites ou les plans soient sécants. Cette notion ne présente d’intérêt que dans l’espace ou lorsqu'on utilise le produit scalaire. On montre qu’une droite est orthogonale à un plan en prouvant qu’elle est orthogonale à deux droites sécantes du plan.
Le plan médiateur d’un segment \([AB]\) passe par son milieu tout en lui étant orthogonal. L’infinité de points qui le composent se trouvent à égale distance de \(A\) et de \(B.\)
Pour terminer cette présentation en géométrie pure, voyons un petit exercice, du niveau de la classe de seconde (ancien programme).
Voici un tétraèdre dans lequel \(AC = AD\) et \(BC = BD.\) Montrer que les droites \((AB)\) et \((CD)\) sont orthogonales.
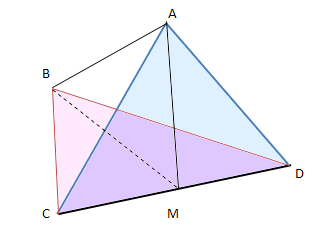
Nous sommes en présence de deux triangles isocèles : les deux arêtes bleues sont de même longueur, ainsi que les deux arêtes rouges. Si l’on place le point \(M,\) milieu de \([CD]\) (segment commun aux deux triangles), les droites \((AM)\) et \((BM)\) sont perpendiculaires à \((CD),\) c’est là une propriété des triangles isocèles. Par conséquent, \((CD)\) est perpendiculaire au plan \((MAB).\) Toutes les droites de ce plan sont donc orthogonales à \((CD),\) y compris \((AB).\) Mais ces deux droites ne sont pas perpendiculaires puisqu’elles ne se coupent jamais.
Et maintenant, graduons…
Passons à l’épisode suivant, celui où les droites découvrent le monde des repères normés (géométrie analytique).
Nous voici dans un espace vectoriel à une dimension (droite), ou deux (plan), ou plus (espaces).
La distance, dite euclidienne, est mesurable par une NORME : \(AB = \| {\overrightarrow {AB} } \|\)
Ainsi, une droite est munie d’un repère comme une règle est munie d’une graduation (« norme » permettant de se « repérer »). Un repère construit grâce à une base de vecteurs non colinéaires est orthogonal si ces derniers sont perpendiculaires et orthonormal si, en plus, ils sont de même norme. Dans un tel repère, la norme d’un vecteur est la suivante (espace à deux dimensions) :
\(\| {\overrightarrow {u}} \| = \sqrt{x^2 + y^2}\)
En univers tridimensionnel on ajoute \(z^2\) sous le radical, et ainsi de suite si l’on travaille sur un nombre supérieur de dimensions (voir le produit scalaire dans l'espace).

Revenons à nos droites et restons pour l’instant dans un banal espace à deux dimensions.
Une droite peut être définie par un point et par une direction. On nomme vecteur directeur un vecteur qui donne à la droite sa direction (il en existe une infinité car la longueur et le sens n'importent pas). Pour démontrer que deux droites sont parallèles ou confondues, on montre que leurs vecteurs directeurs sont colinéaires (voir la page colinéarité dans le plan, rédigée pour les élèves de seconde).
Relations fonctionnelles
Dans le plan muni d'un repère, la droite est la traduction d'une fonction affine qui exprime une relation entre deux variables numériques.
Une droite peut être définie de trois façons. Celle qui est enseignée dès le collège est l'équation réduite sous forme (\(y = ax + b\) où \(a\) est le coefficient directeur et \(b\) est l'ordonnée à l'origine). L'équation cartésienne s'écrit quant à elle sous la forme \(αx + βy + δ\) \(=\) \(0.\) Elle permet davantage de développements, surtout si l'on quitte le plan pour une étude dans l'espace. Une troisième façon est de définir une droite par l'un de ses points et par l'un de ses vecteurs directeurs. Si les paramètres de la droite sont des nombres rationnels, on parle de droite rationnelle.
Ainsi, pour montrer que deux droites sont parallèles, il suffit que les coefficients directeurs des deux fonctions soient les mêmes et pour trouver en quel point du plan deux droites sont sécantes, il suffit de résoudre un système de deux équations à deux inconnues qui sont l'abscisse et l'ordonnée communes aux deux droites. Enfin, deux droites sont perpendiculaires si le produit de leurs coefficients directeurs est égal à -1.
Par ailleurs, une droite dans un plan ne représente pas toujours la fonction elle-même. Ce peut être une tangente ou une asymptote...
Toutefois, les droites ne sont pas ici des objets d'étude en elles-mêmes mais des outils qui facilitent une étude, parfois abstraite ou parfois très concrète. La page d'introduction à la programmation linéaire montre qu’une problématique réelle d’allocation peut être résolue par un système d’inéquations et être visualisée graphiquement.
Dans un espace à trois dimensions, les droites se définissent comme une intersection entre deux plans, c’est-à-dire que leur expression prend la forme d’un système de deux équations cartésiennes. Si le nombre de dimensions est plus élevé, on est amené à résoudre des systèmes plus volumineux. En l’absence regrettable de logiciel, on peut utiliser la méthode du pivot de Gauss pour en venir à bout.
C’est tout pour cette partie théorique...
