Applications ou fonctions
Cette page s'adresse surtout aux étudiants de première année (filières économiques) qui retrouvent une branche des mathématiques sur laquelle ils ont déjà longuement travaillé dans le secondaire, mais avec une approche un peu plus globale. Si vous devez vous rafraîchir la mémoire, révisez en commençant par la page d'initiation aux fonctions.
C'est Leibniz qui aurait employé ce terme de « fonction » en premier, bien que la notion était plus ou moins exprimée depuis les Babyloniens.
Applications
Une bonne partie du domaine mathématique concerne l'étude de relations. Celles-ci peuvent exister au sein d'un même ensemble (voir les structures algébriques ou éventuellement un outil pratique avec l'algorithme de Djikstra) mais plus souvent entre deux ensembles, qu'ils soient numériques ou non. Ce sont des relations binaires.
Sous condition, ces dernières peuvent être des applications. Quelle condition ? Une application est une relation qui associe TOUT élément d’un ensemble de départ (un antécédent) à un seul élément d’un ensemble d’arrivée (une image).
Application et fonction sont en principe synonymes mais certains donnent au terme fonction un sens moins restrictif : par commodité de langage, ils parlent de fonction même si un ou plusieurs éléments de l'ensemble de départ n'ont aucun élément associé dans celui d'arrivée ; il faut donc préciser l'ensemble (ou domaine) de définition de la fonction, c'est-à-dire l'ensemble des valeurs pour lesquelles la relation existe. Dans les faits, il existe surtout une distinction d'usage entre les deux termes : lorsque l'application est numérique, il est plus habituel d'employer le nom fonction.
Quant il s'agit d'une fonction numérique, l'ensemble de départ est souvent constitué d'un intervalle de réels. S'il s'agit de celui des entiers naturels, on la nomme suite (ou série, qui est la somme des premiers termes d'une suite).
Il est fréquent d'appeler \(f\) l’opérateur d'une fonction. L'image d'un argument \(x\) est alors le réel \(f(x).\) Formellement, l'image de \(A\) (partie de l'ensemble de départ \(E\)) par \(f\) est l'ensemble \(f(A)\) :
\(f(A) = \{y \in F | \exists x \in A\) tel que \(y = f(x) \}\)
Définitions : \(f\) est une fonction définie sur un ensemble \(D\) de nombres réels si à chaque valeur \(x\) de \(D\) est associé un nombre réel unique noté \(f(x)\) ou, pour reprendre la définition de Lobatchevski, « par fonction d'une variable, on fait référence à une grandeur dont la valeur dépend de cette variable ».
Dans le secondaire, les études de fonctions numériques représentent une part importante des programmes de maths. Mais l'étude des applications est beaucoup plus étendue. Ainsi, lorsqu'une application a pour ensemble d'arrivée un corps, on parle de forme. Par exemple, une fonction déterminant est une forme d'un espace vectoriel sur un ensemble de scalaires (des réels ou des complexes). Par ailleurs, une variable aléatoire et une loi de probabilité sont aussi des fonctions.
Représentation graphique
Graphiquement, une fonction d'une variable est représentée par une courbe dans un plan muni d'un repère (on l'appelle courbe même si c'est une droite). Les antécédents figurent en abscisse (\(x\)) et leurs images sont lues sur l’axe des ordonnées (\(y\)). À chaque valeur de \(x\) appartenant à l'ensemble de définition est associée \(y,\) valeur prise par \(f(x).\) Voici un exemple de courbe représentant une relation dans \(\mathbb{R}^2\) qui N’EST PAS une application puisqu'à certaines valeurs de \(x\) correspondent jusqu'à trois valeurs de \(y\) :
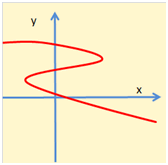
En économie, ce type de courbe n'est pas rare (illustration en page de frontière efficiente). Il représente les différentes solutions admises par une équation.
Propriétés
Avant de revenir aux fonctions numériques, voyons quelles propriétés peuvent présenter les applications.
Injection : une application est injective si deux éléments distincts de l’ensemble de départ ont deux images distinctes. Tous les détails sur la page qui traite spécifiquement de l'injection.
Surjection : une application est surjective lorsque l’ensemble d’arrivée est entièrement couvert. À titre d'exemple, si l’on considère que l'ensemble d’arrivée est \(\mathbb{R}^*_+,\) la fonction exponentielle est surjective mais pas si cet ensemble d'arrivée est \(\mathbb{R}.\)
Illustration d'une représentation de surjection dans \(\mathbb{R}^2\) :
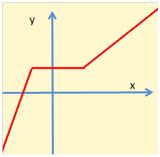
Sur les concepts d'injection et de surjection, voir aussi la page rang et noyau.
Bijection : une bijection est injective ET surjective. Situation facile à appréhender (chaque antécédent a une seule image et vice versa). Une application bijective admet une réciproque.
Ces notions sont illustrées en page de diagrammes sagittaux.
Opérations sur les fonctions
Des applications \(f\) et \(g\) peuvent s’enchaîner. Le résultat est une autre application, dite composée de fonctions et notée \(f \circ g.\) Là aussi, illustration en page de diagrammes sagittaux.
Les fonctions peuvent également s'ajouter ou se multiplier, soit entre elles soit avec des scalaires (Cf. les opérations sur les fonctions).
Fonctions numériques usuelles
Ce sont les fonctions numériques de base, sur lesquelles se greffent toutes les fonctions numériques par le jeu de la composition.
La fonction constante est la plus triviale puisqu'à tout antécédent est associée la même image. Les fonctions linéaires et affines se traduisent graphiquement par des droites (d'ailleurs toute droite du plan peut représenter une fonction, sauf si elle est verticale puisque dans ce cas on associe une infinité d'images à un seul antécédent).
Parmi les applications enseignées avant la classe de terminale, mentionnons les fonctions : carré et cube, inverse, racine carrée. La fonction valeur absolue fait aussi partie de ces applications simples.
Les fonctions obtenues par addition, soustraction, multiplication, division et élévation à la puissance sont dites algébriques (polynomiales, homographiques, avec racines carrées...).
Les fonctions trigonométriques et les trigonométriques réciproques sont aussi des fonctions usuelles.
La grande famille des fonctions logarithmes et exponentielles constitue également un excellent vivier de fonctions usuelles : logarithme népérien, décimal ou de base a, exponentielle, exponentielle de base a, les quatre hyperboliques, les hyperboliques réciproques, etc.
Ces fonctions, non algébriques, sont dites transcendantes.
Étude d'une fonction numérique : voir la page sur l'étude de fonction.
Utilité
Les fonctions servent dans une quantité inombrable de domaines et de circonstances. L'objet de ce site web étant d'ordre économique, nous ne survolerons ici que quelques applications (au sens commun du terme) en sciences économiques et de gestion.
En statistiques, on étudie des relations qui ne sont pas toujours des fonctions. Des grandeurs observées sont représentées par ces incontournables nuages de points que le data analyst résume par une fonction (Excel suffit souvent pour le faire) dans un dessein prédictif ou prévisionnel. L'expression la plus simple est l’équation d'une droite de régression linéaire. Mentionnons aussi la régression sur tendance quadratique, sur tendance exponentielle, sur tendance logarithmique, sur tendance logistique, sur courbe de Gompertz... Notez qu'une mesure de probabilité est une application d'une tribu vers \([0\,; 1]\) et qu'une variable aléatoire (ainsi qu'une variable statistique) est elle aussi une application, et non une variable au sens mathématique. Une variable aléatoire n'est pas notée \(f\) mais le plus souvent \(X.\)
En gestion ou en marketing, on rencontre quelques types de fonctions sous forme d'équation pour, par exemple, déterminer un coût marginal ou une élasticité-prix. Voir aussi la page exercice sur les surplus. Un questionnaire rempli dans le cadre d'une étude de marché ne constitue pas une application dès lors que plusieurs réponses sont autorisées pour une question.
En économie et plus rarement en gestion, on étudie des fonctions de deux variables.
