Présentation et exercices sur la valeur absolue
L’étude de la fonction « valeur absolue » fait partie du programme de première générale mais elle semble assez souvent occultée...
La notion de valeur absolue est simple à comprendre et on l'aborde désormais en classe de seconde (voir la page sur les distances entre réels).
Présentation
La valeur absolue d’un réel \(x\) est le nombre noté \(|x|.\) Il est égal à \(x\) si celui-ci est positif et à \(–x\) s’il est négatif. Par conséquent, une valeur absolue est toujours positive (ou nulle). Par exemple, \(|3| = 3\) et \(|-3| = 3.\) Il est également évident que si \(|x| = |y|,\) alors \(x = y\) ou \(x = -y\) ou encore que \(|x| × |y| = |xy|.\) Enfin, \(\sqrt{x^2} = |x|.\)
Ces chères valeurs absolues squattent aussi un chapitre de géométrie. En effet, par nature, une distance est positive.
Inégalité triangulaire
Une propriété intéressante de la valeur absolue est l’inégalité triangulaire :
\(|x + y| \leqslant |x| + |y|\)
Si \(x\) et \(y\) sont de même signe, il y a égalité. En revanche, s’ils sont de signe contraire, il y a inégalité stricte. Soit par exemple \(x = 2\) et \(y = -3.\) Nous avons \(|x + y| = 1\) alors que \(|x| + |y| = 5.\)
Là aussi, on retrouve cette propriété lorsqu’on étudie les distances.
Fonction valeur absolue
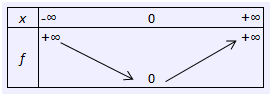
La fonction est définie sur \(\mathbb{R}\) par \(x \mapsto |x|.\) C’est une fonction paire.
Sens de variation : strictement décroissante sur \(]-\infty\,;0[\) et strictement croissante sur \(]0\,;+\infty[.\)
Représentation graphique obtenue avec une calculatrice en ligne gratuite (grapheur.cours-de-math.eu) :
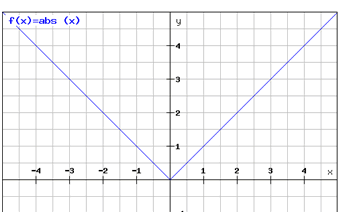
Dérivée : la fonction valeur absolue est dérivable partout sauf pour \(x = 0.\)
Soit la fonction \(f\) telle que \(f(x) = |x|,\) alors pour tout \(x \in ]-\infty\,;0[,\) sa dérivée s'écrit \(f’(x) = -1\) et pour tout \(x \in ]0\,;+\infty[\) nous avons \(f’(x) = 1.\)
Exercice 1
Résoudre algébriquement l’équation \(|x + 2| = |x - 4|\)
Exercice 2
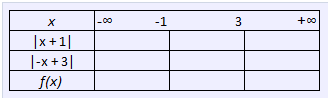
Soit \(f\) une fonction définie sur \(\mathbb{R}\) par \(f(x) = |x + 1| + |-x + 3|\)
- Compléter le tableau suivant en indiquant les expressions de \(|x + 1|\) et de \(|-x + 3|\) sans valeurs absolues.
- Dresser le tableau de variation de la fonction puis tracer sa courbe représentative \({\mathscr{C}_f}.\)
- Résoudre l’inéquation \(f(x) < 6\) puis vérifier le résultat sur le graphe.
Corrigé 1
Pour résoudre cette équation, il faut se souvenir que si \(|x| = |y|,\) alors \(x = y\) ou \(x = -y.\)
Donc \(x + 2 = x - 4\) ou \(x + 2 = -x + 4\)
Il est évident que la première équation n’a pas de solution. En revanche, la seconde équation en a une : \(x = 1.\) Donc il existe une unique solution \(S = \{1\}.\)
Corrigé 2
1- Tableau complété.

2- On constate que \(f\) est une fonction affine par morceaux, d’abord décroissante (coefficient directeur négatif : -2), puis constante, puis croissante.
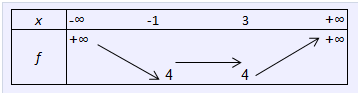
3- Résolvons l’inéquation \(|x + 1| + |-x + 3| < 6.\) Pour cela, rappelons les expressions de \(f.\)
\[\left\{ {\begin{array}{*{20}{c}} { - 2x + 2\; {\rm{si }}\;x \in\; ] - \infty \,;-1]}\\ {4\; {\rm{si }}\;x \in [ - 1\,;3]}\\ {2x - 2\; {\rm{si }}\;x \in [3\,; + \infty ]} \end{array}} \right.\]
\(-2x + 2 < 6\) équivaut à \(x > -2,\) donc l’intervalle \(]-2\,;-1]\) convient.
L’intervalle \([-1\,;3]\) convient également puisque \(f(x) = 4\)
\(2x - 2 < 6\) équivaut à \(x < 4,\) donc l’intervalle \([3\,;4[\) convient aussi.
Par conséquent, \(S =\; ]-2\,; 4[\)
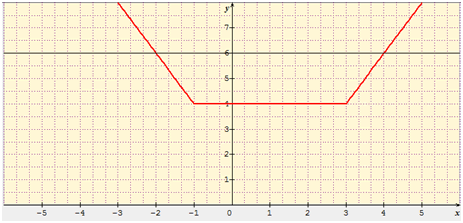
Nous vérifions bien sur le graphe que la courbe est au-dessous de \(y = 6\) pour les valeurs de \(x\) comprises entre -2 et 4.
