Ensembles de définition, extremums, signes...
Si vous êtes en classe de seconde, cette page a été écrite pour vous. Elle fait le point sur les concepts qu’il faut connaître pour aborder l’étude des fonctions. Ce vaste domaine mathématique appelé « analyse » devrait d'ailleurs vous accompagner pendant quelques années encore.
L’ensemble de définition
C’est l’ensemble des variables \(x\) pour lesquelles une fonction est définie. Vous connaîtrez deux situations. Soit il vous est donné, soit vous devez le déterminer.
S’il est précisé dans l’énoncé, pas de souci. Il s’agit d’un intervalle. Par exemple, \(x \in [0\,;20].\) Il peut aussi être lu sur une courbe (voir l’exercice de la page lien entre fonction et courbe).
S’il n’est pas donné, il s’impose soit par les données du problème, soit par des interdits mathématiques.
Un problème concret se situe dans un cadre donné. Celui-ci détermine l’intervalle. Par exemple, si l’on mesure la vitesse d’une voiture départ arrêté pendant 60 secondes, considérez que l’ensemble de définition est \([0\,;60].\)
En classe de seconde, on connaît deux interdits mathématiques : un dénominateur doit être différent de 0 et une racine carrée ne s’applique qu’à un nombre positif ou nul. Ceci suffit pour déterminer vous-même certains ensembles de définition.
Exemple 1 : soit la fonction \(f\) définie par \(f(x) = \frac{x^2}{5x + 10}\) et soit \(E\) son ensemble de définition.
Il faut alors poser l’équation \(5x + 10 = 0\)
\(⇔ 5x = -10\)
\(⇔ x = -2\)
Par conséquent l’ensemble de définition \(E\) est l’ensemble des réels sauf un : -2. Cela s’écrit \(\mathbb{R} \backslash \{-2\}\) ou éventuellement sous forme d’intervalle : \(]-\infty ; -2[ \cup ]-2\,; +\infty[.\) Cette astuce qui consiste à ouvrir deux crochets pour éliminer une valeur est très courante en maths et il vaut mieux s’y habituer dès maintenant ! (note : attention à ne pas dire que l’ensemble de définition est -2).
Exemple 2 : soit la fonction \(g\) définie par \(g(x) = \sqrt{5x + 10}\) et soit \(D_g\) son ensemble de définition.
Il faut alors poser l’inéquation \(5x + 10 \geqslant 0\)
\(⇔ 5x \geqslant -10\)
\(⇔ x \geqslant -2\)
Contrairement à l’exemple précédent, nous obtenons directement l’ensemble de définition. Ici, on écrit \(D_g = [-2\,;+\infty[.\)
La courbe
La représentation graphique d’une fonction est appelée courbe même si son tracé n’est pas courbé. Notée par exemple \(C_f,\) il ne faut pas la confondre avec la fonction elle-même. Dans un repère, la variable \(x\) figure en abscisse. Les valeurs prises par la fonction sont lues sur l’axe des ordonnées (\(y\)). Voir la définition d'une courbe en page fonction et sa représentation sur calculatrice en page tracé de courbe avec calculatrice TI.
Antécédents et images
Les notions d'image et d'antécédent ont disparu du programme de seconde mais vous pouvez tout de même les rencontrer.
Soit une fonction \(f.\) Toute valeur de \(x\) sur son ensemble de définition possède une image et une seule par \(f.\)
Une valeur donnée \(y,\) lue graphiquement sur l’axe des ordonnées, peut ne pas avoir d’antécédent par \(f\) ou en avoir un, ou encore plusieurs… On le visualise lorsqu’on trace une droite horizontale en \(y\) : il suffit de compter combien de fois cette droite traverse la courbe. Voir la page antécédents et images.
Le sens de variation
Sur un intervalle, une fonction peut être croissante, décroissante ou constante. Sa courbe est orientée vers le haut, vers le bas ou vers l’horizontale et il est généralement facile de repérer graphiquement le sens de variation d’une fonction. Attention, on parle bien du sens de variation de la FONCTION et non de sa courbe représentative. Voir la page sur le sens de variation.
Le tableau de variation
Voir la page sur le tableau de variation.
L’extremum
L’extremum est soit un maximum, soit un minimum. C’est une notion assez intuitive mais il vaut mieux la définir avec rigueur… Graphiquement, on parle de sommet.

Soit \(f\) une fonction définie sur \(E,\) soit \(I\) un intervalle de \(E\) et soit \(a\) un nombre appartenant à \(I.\)
Dire que \(f\) admet un maximum en \(a\) sur \(I\) signifie que \(f(a)\) est la plus grande valeur prise par la fonction sur \(I.\) Autrement dit, pour tout \(x\) de \(I,\) \(f(x) \leqslant f(a).\)
Dire que \(f\) admet un minimum en \(a\) sur \(I\) signifie que \(f(a)\) est la plus petite valeur prise par la fonction sur \(I.\) Autrement dit, pour tout \(x\) de \(I,\) \(f(x)\geqslant f(a).\)
Les extremums apparaissent sur le tableau de variation.
Note : plus d'informations en page extremums, mais non destinées aux élèves de seconde. En revanche, vous pouve faire les exercices sur les extremums.
Le tableau de signes
Une première approche du tableau de signes est réalisée à partir d’une courbe ou parfois d’un tableau de variation (encore qu’il est généralement impossible de faire le lien entre les deux lorsqu’on ignore l’équation de la fonction).
Ce tableau résume dans quels intervalles une fonction est négative, positive ou nulle.
Exemple :
Soit une fonction \(f\) définie sur \(\mathbb{R}\) et représentée par la courbe suivante :
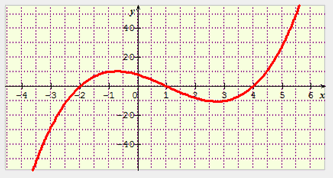
Quel est le signe de \(f\) ?
Pour réaliser le tableau de signes, il suffit de se suivre l’axe des abscisses de gauche à droite et de relever en quels points la courbe passe au-dessus ou au-dessous de l’axe.
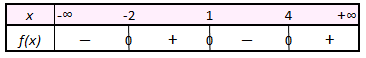
Le tableau indique que la fonction prend trois fois la valeur nulle. On peut l’exprimer de plusieurs façons : « 0 a trois antécédents par \(f\) », « \(f(x) = 0\) admet trois solutions » ou encore « la courbe représentative de \(f\) traverse trois fois l’axe des abscisses ».
