Exercices sur extremums (niveau seconde)
Cette page vous propose deux exercices de niveau seconde sur les extremums de fonctions. Le premier est très rapide (le tableau de variation figure d'ailleurs au programme) tandis que le deuxième met en œuvre des connaissances assez diverses…
Énoncés
Exercice 1 : racine carrée
Soit \(f\) la fonction racine carrée. Tracer son tableau de variation puis déterminer, s'ils existent, son minimum et son maximum.
Exercice 2 : problème de géométrie
Soit \(ABC\) un triangle rectangle en \(A,\) avec \(AB = 4\) et \(AC = 5.\) Soit trois points \(D,\) \(E\) et \(F\) situés respectivement sur \([AB],\) \([BC]\) et \([AC]\) tels que \(ADEF\) est un rectangle.
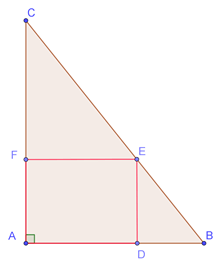
La longueur \(FC\) est notée \(x.\)
1- Exprimer \(EF\) en fonction de \(x.\)
2- Montrer que l'aire de \(ADEF\) est égale à \(0,8x(5 – x)\)
3- Soit la fonction \(f\) définie par \(f(x) = 0,8x(5 – x).\) Compte tenu des dimensions du rectangle, quel est l'ensemble de définition de \(f\) ?
4- Déterminer le maximum de \(f\) avec la calculatrice.
5- Quelles sont les dimensions du rectangle \(ADEF\) pour que son aire soit maximale ?
6- Tracer la figure avec GeoGebra.
Corrigé 1
La fonction racine carrée étant strictement croissante sur \([0\,; +\infty[,\) son tableau de variation est particulièrement simple.
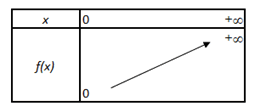
Elle admet un minimum en 0 (il est égal à 0) mais aucun maximum puisqu'elle s'élève dans les territoires infinis…
Corrigé 2
1- Avec ce triangle rectangle de toute beauté, on s'attend à avoir besoin du théorème de Pythagore. Eh bien non ! C'est celui de Thalès qui va nous aider.
Dans le triangle \(ABC,\) \(F\) est un point de \(AC\) et \(E\) est un point de \(BC.\) De plus, les droites \((EF)\) et \((AB)\) sont parallèles.
Donc, selon le théorème de Thalès, \(\frac{EF}{AB} = \frac{CF}{AC}\)
Nous savons que \(AB = 4\) et \(AC = 5.\)
\(\frac{EF}{4} = \frac{x}{5}\)
\(\Leftrightarrow EF = 0,8x\)
2- L'aire d'un rectangle est égale à sa longueur multipliée par sa largeur, comme vous le savez depuis votre tendre enfance.
\(EF \times AF = 0,8x(5 - x)\)
3- Si \(F\) est confondu avec \(C,\) alors \(x = 0.\) Si \(F\) est confondu avec \(A,\) alors \(x = 5.\) L'ensemble de définition de la fonction \(f\) est \([0\,; 5].\)
4- Les modes d'emploi des calculatrices se trouvent sur la page consacrée aux courbes (avec des détails supplémentaires en page courbes avec TI pour les Texas Instrument et fonction inverse pour les Casio).
Pour connaître les coordonnées du maximum avec une TI, c'est avec la touche calculs (c'est-à-dire 2nde puis trace) puis le choix « 4 : maximum »
Avec une Casio, touches F5 puis F2. Illustration avec une GRAPH35+
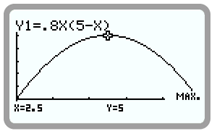
Le maximum est égal à 5. Il est obtenu pour une valeur de \(x\) de 2,5.
5- L'aire maximale de \(ADEF\) étant égale à 5 pour \(FC = 2,5,\) donc pour \(AF = 5 - 2,5 = 2,5,\) alors \(AD = 2.\) Les dimensions du rectangle sont \(2 \times 2,5.\)
6- Ouvrez GeoGebra. Comme vous n'aurez pas besoin des axes, vous pouvez les effacer (clic droit sur la feuille, puis décochez Axes). Le bouton qui sert à tracer les figures telles que les triangles est celui-ci :

Positionnez-vous à l'intersection sur une intersection de quatre carreaux (pour la facilité !). Cliquez et ce sera le point \(A.\) Déplacez-vous vers la droite de quatre carreaux, cliquez et voilà votre \(B\). Puis placez \(C\) et à la fin recliquez sur \(A\) pour finir la figure.
Vous avez votre triangle rectangle. Vous pouvez à présent placer les points \(E,\) \(D\) et \(F.\) Le bouton « Point sur Objet » est parfait pour cela.

Il reste à tracer le rectangle comme vous l'avez fait pour le triangle.
Pour des raisons esthétiques, vous souhaitez peut-être supprimer les étiquettes qui s'affichent automatiquement (les noms des segments). Vous pouvez faire des clics droits soit sur la figure soit sur les coordonnées à gauche et désélectionner « Afficher l'étiquette ». Si vous souhaitez changer une couleur, faites de même mais, toujours dans le menu contextuel, cliquez sur « Propriétés… »
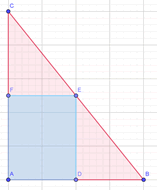
Parmi les coordonnées, vous trouverez certainement q1 = 5. C'est l'aire du quadrilatère (que l'on a déterminée à la question 4).
