Positions dans l'espace, médianes et théorème de Thalès
Cette page ô combien passionnante présente quelques notions de géométrie dans l’espace (donc en trois dimensions).
Il est assez intuitif de deviner ce que fabriquent des points, des droites et des plans dans l’espace mais pour être sûr de bien fixer les idées, récapitulons-le.

Points, droites et plans
Il ne peut passer qu’une seule droite par deux points (c’est aussi valable dans un plan à deux dimensions).
Par trois points non alignés il passe un plan unique. Du coup, trois points suffisent pour définir un plan.
Si deux points sont situés dans un plan, alors tous les points de la droite qui les inclut font aussi partie du même plan. C’est assez évident mais il est utile de s’en souvenir pour démontrer les intersections de plans. N’oublions pas que les chapitres de géométrie de seconde permettent aux élèves de développer des capacités de démonstration, bien utiles pour qui veut suivre ensuite un parcours scientifique (Note : la plupart des autres s’en fichent puisqu’ils ne rencontreront plus de géométrie jusqu’au bac).
Des points ou des droites qui font partie d’un même plan sont dits coplanaires.
Il découle de tout ceci qu’un plan peut être défini soit par trois points, soit par un point et une droite, soit par deux droites (peu importe d’ailleurs que celles-ci soient sécantes ou parallèles).
Deux plans peuvent être confondus, parallèles ou sécants. S’ils sont sécants, ils le sont selon une droite (voir la page sur les droites et plans sécants).
Idem entre une droite et un plan : la droite est soit incluse dans le plan, soit parallèle, soit sécante (en un point).
Enfin, dans l’espace, deux droites sont coplanaires ou non. Dans l’affirmative, elles sont soit confondues, soit parallèles, soit sécantes.
Un type d'exercice faisant intervenir quelques unes de ces propriétés est la section d'un polyèdre. Un autre type d'exercice est présenté ci-dessous.
Exercice (intersection d’une droite et d’un plan)
Soit un tétraèdre (solide à quatre faces triangulaires, pas nécessairement identiques) \(ABCD\) et soit \(G\) le centre de gravité de \(ABC.\) Soit \(M\) le milieu de \([AD].\) Déterminer l’existence d’un point d’intersection \(I\) entre la droite \((MG)\) et le plan \((BCD).\)
Rappels préalables
Le centre de gravité d’un triangle se trouve à l’intersection des trois médianes. Une médiane est une droite qui passe par un sommet et par le milieu du côté opposé. Quel que soit le triangle, ses trois médianes sont concourantes.
Une médiane coupe donc un triangle en deux aires égales.
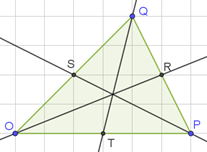
Le théorème de Thalès est également un acquis du collège. Ce n’est pas une raison pour ne pas en rappeler toute la saveur.
Soit un triangle \(ABC,\) et deux points \(D\) et \(E\) situés sur les droites \((AB)\) et \((AC)\) de façon que \((DE)\) soit parallèle à \((BC).\) Alors :
\(\frac{AD}{AB} = \frac{AE}{AC} = \frac{DE}{BC}\)
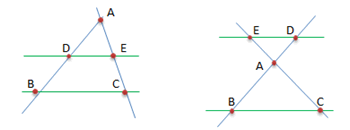
Inversement, la réciproque du théorème de Thalès démontre que si ces rapports sont égaux, alors il y a parallélisme. Un cas particulier est connu sous le nom de théorème des milieux : si une droite passe par les milieux de deux côtés d'un triangle, alors elle est parallèle au troisième côté. Vous en trouverez une application étonante en page du théorème de Varignon.
Corrigé
Il s’agit d’un exercice classique, qu’il n’est pas rare de trouver dans un manuel ou de découvrir lors d’un contrôle ! Dessinons d’abord le tétraèdre (sur Geospace).
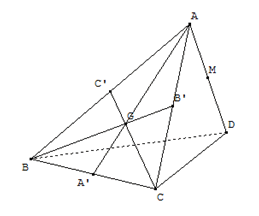
Soit le triangle \(AA’D.\) Nous savons que les points \(AGA’\) et \(AMD\) sont alignés. Comme \(M\) est le milieu de \([AD]\) et \(AG = \frac{2}{3} AA’\) (propriété des médianes vue plus haut), nous avons :
\(\frac{AG}{AA'} = \frac{2}{3}\) et \(\frac{AM}{AD} = \frac{1}{2}\)
La réciproque du théorème de Thalès nous permet de conclure que les droites \((MG)\) et \((DA’)\) ne sont pas parallèles.
Comme \(A\) appartient à la droite \((BC),\) il appartient aussi au plan \((BCD).\) Donc la droite \((MG)\) est bien sécante à \((BCD)\) en un point qu’il n’est pas interdit de nommer \(I.\)
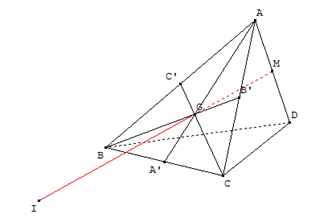
Fin de l’histoire.
