Démonstrations du théorème de Varignon
Le théorème de Varignon ne fait pas partie des programmes officiels mais il fait parfois l’objet d’un exercice en classe de seconde. Après avoir rapidement fait connaissance avec Varignon, nous exposerons son théorème puis nous verrons comment le prouver de deux façons différentes.
Qui était Varignon ?
Pierre Varignon était… un prêtre. Il est né en 1654 à Caen, à une époque où les hommes d’Église étaient à peu près les seuls à trouver le temps de réfléchir aux problématiques mathématiques et physiques. Louis XIV le nomma premier titulaire de section de géométrie de l’Académie royale.

Ses contributions à la science furent très diverses. Il fit connaître en France les travaux de Newton et de Leibniz (si vous êtes en seconde, attendez l’année prochaine pour prendre la mesure d’un tel évènement) et il montra le lien mathématique entre vitesse et accélération. Il inventa le manomètre, qui n’avait pas encore la forme qu’on lui connaît lorsqu’il sert à mesurer la pression des pneus !
Curieusement, son nom est surtout associé au théorème qu’il a formalisé mais qui était sans doute connu depuis longtemps. Un théorème qui n’a rien révolutionné mais qui démontre une propriété amusante des quadrilatères.
Le théorème
Soit \(ABCD\) un quadrilatère quelconque et \(I, J, K, L\) les milieux de ses côtés. Alors \(IJKL\) est un parallélogramme.
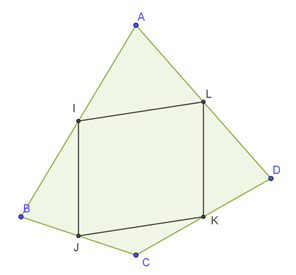
Ci-dessous nous utiliserons les points tels qu’indiqués sur cette figure réalisée avec GeoGebra.
Les corollaires à ce théorème sont que l’aire de \(ABCD\) est le double de celle de \(IJKL\) (que nous ne démontrerons pas) et que les médianes d’un quadrilatère quelconque ont le même milieu (qui se trouve bien sûr où les diagonales de \(IJKL\) se croisent).
Vecteurs
\(I\) est le milieu de \([AB]\) donc \(\overrightarrow {AB} = 2\overrightarrow {IB} \)
\(J\) est le milieu de \([BC]\) donc \(\overrightarrow {BC} = 2\overrightarrow {BJ} \)
Par la relation de Chasles nous en déduisons que \(\overrightarrow {AC} = 2\overrightarrow {IJ} \)
\(L\) est le milieu de \([AD]\) donc \(\overrightarrow {AD} = 2\overrightarrow {LD} \)
\(K\) est le milieu de \([DC]\) donc \(\overrightarrow {DC} = 2\overrightarrow {DK} \)
Par la relation de Chasles nous en déduisons que \(\overrightarrow {AC} = 2\overrightarrow {LK} \)
Nous avons montré que \(\overrightarrow {AC} \) est à la fois égal à \(2\overrightarrow {IJ} \) et à \(2\overrightarrow {LK} .\) On en conclut sans mal que \(\overrightarrow {IJ} = \overrightarrow {LK} \)
D’après la règle du parallélogramme, \(IJKL\) est donc un parallélogramme.
Théorème des milieux
L’autre démonstration peut être découverte dès le collège puisque c’est une simple application du théorème de Thalès.
\(I\) est le milieu de \([AB]\) donc \(AI = \frac{1}{2}AB.\)
\(L\) est le milieu de \([AD]\) donc \(AL = \frac{1}{2}AD.\)
Rappelons le théorème des milieux : si une droite passe par les milieux de deux côtés d'un triangle, alors elle est parallèle au troisième côté. Donc \((IL)\) est parallèle à \((BD).\)
De la même façon, on montre que \((JK)\) est parallèle à \((BD)\) et il s’ensuit que \((IJ)\) et \((JK\) sont parallèles.
En suivant le même raisonnement, on montre que les droites \((LK)\) et \((IJ)\) sont parallèles à \((AC)\), donc parallèles entre elles.
Ainsi \(IJKL\) est bien un parallélogramme.
Avec un quadrilatère croisé
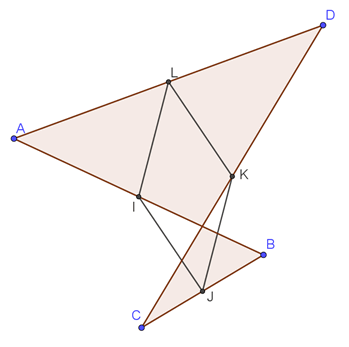
Le théorème des milieux fonctionne dans un triangle mais aussi dans une configuration en papillon (voir la page sur le théorème de Thalès). Vous ne serez donc pas étonné de constater que le théorème de Varignon s’applique aussi aux quadrilatères croisés.
D’ailleurs en voici un.
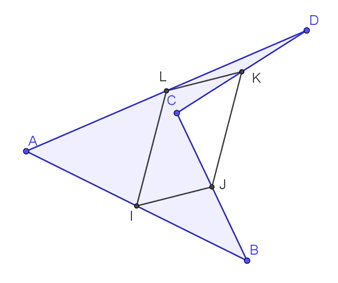
Avec un quadrilatère concave
Et mesdames et messieurs de plus en plus fort ! Avec un quadrilatère concave !
Quel talent, ce Varignon.
