Plan dans l'espace et coplanéarité
Vous êtes en terminale et vous vous apprêtez à explorer l'espace. Votre voyage débute ici. Il comportera deux escales : la caractérisation d’un plan et les vecteurs coplanaires. Cet espace ne comportant aucun repère, vous êtes priés de ne pas décrocher (le repérage dans l’espace fait l’objet d’une autre page).
Un plan dans l’espace
On peut définir un plan par un point et deux vecteurs non colinéaires.
Soit un point \(O\) de l’espace et deux vecteurs \(\overrightarrow i \) et \(\overrightarrow j \). On détermine les points \(I\) et \(J\) tels que \(OI = \overrightarrow i \) et \(OJ = \overrightarrow j \) ce qui permet de définir un plan \((OIJ)\). N’importe quel point de ce plan, dirigé par le couple \((\overrightarrow i \,;\overrightarrow j )\), peut être exprimé en fonction de \(\overrightarrow i \) et \(\overrightarrow j \).
Une représentation graphique de cette propriété ne serait pas très parlante sur votre écran mais si vous avez du mal à vous représenter des vecteurs dans l’espace, une photo peut vous aider.

L’œil de la colombe est le point \(O\). Le bec est un vecteur \(\overrightarrow i \), parallèle à votre écran. La queue est un vecteur \(\overrightarrow j \) qui semble venir vers vous.

Le point \(O\) et les vecteurs \(\overrightarrow i \) et \(\overrightarrow j \) définissent un plan \(\mathscr{P}.\)

Exemple. Soit le point \(A(3\,;2)\). Nous avons \(\overrightarrow {OA} = 3\overrightarrow i + 2\overrightarrow j \)
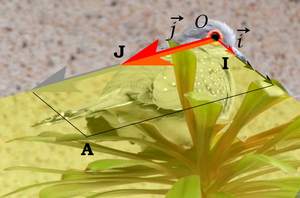
Ci-dessus, seul un quart du plan a été représenté. On peut imaginer qu’au-dessus de ce plan incliné passant par l’œil de la colombe émergeraient quelques feuilles…
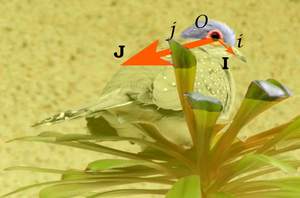
Bon, assez joué avec Photoshop, passons aux vecteurs coplanaires.
Vecteurs coplanaires
Intuitivement, on devine que des vecteurs sont dit coplanaires si, et seulement si, ils sont dans le même plan. Formulons-le autrement.
Soit trois vecteurs de l’espace \(\overrightarrow u \), \(\overrightarrow v \) et \(\overrightarrow w \). Ils sont coplanaires s’il existe trois réels \(\alpha\), \(\beta\) et \(\gamma\) tels que \(\alpha \overrightarrow u + \beta \overrightarrow v + \gamma \overrightarrow w = \overrightarrow 0 \).
Ces réels ne doivent pas tous être égaux à zéro.
Deux vecteurs sont toujours coplanaires (c’est assez évident). Ainsi, si parmi trois vecteurs deux sont colinéaires, alors les trois sont coplanaires.
Remarquez que si l’égalité ci-dessus se vérifie avec trois réels, elle se vérifie avec une infinité (à l’instar d’une équation cartésienne de droite, on peut multiplier les deux membres de l'égalité par n'importe quel réel). En revanche, on peut déterminer si des vecteurs sont coplanaires en vérifiant une combinaison linéaire unique \(\overrightarrow w = \alpha \overrightarrow u + \beta \overrightarrow v \).
Et les points ? Trois points de l’espace sont toujours coplanaires. Mais pour vérifier que quatre points \(A\), \(B\), \(C\) et \(D\) le sont, il faut montrer que les vecteurs \(\overrightarrow {AB} \), \(\overrightarrow {AC} \) et \(\overrightarrow {AD} \) le sont.
Coordonnées
Si trois vecteurs \(\overrightarrow i \), \(\overrightarrow j \) et \(\overrightarrow k \) ne sont pas coplanaires, ils définissent un espace dans lequel un vecteur \(\overrightarrow u \) a des coordonnées uniques (voir la page sur le repérage dans l'espace).
\[\overrightarrow u = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \]

Un exemple célèbre
Au dix-neuvième siècle, le physicien écossais James Clerk Maxwell considéra trois vecteurs non coplanaires correspondant aux couleurs primaires (rouge, vert et bleu). Il comprit que toute couleur pouvait être définie comme un vecteur dans l'espace, combinaison linéaire des trois primaires (en fait, il les représentait dans un triangle). En 1861, Maxwell obtint la première photographie en couleurs. L'écran que vous êtes en train de regarder fonctionne sur ce principe puisqu'un pixel peut être considéré comme un vecteur de dimension 3 codé en hexadécimal.
