Introduction aux vecteurs dans l'espace
Ce que vous avez appris sur les vecteurs dans le plan depuis la classe de seconde, vous allez à présent le transposer dans l’espace. L'occasion de réinvestir de ce vous savez déjà. Par exemple, la relation de Chasles s’applique, la définition de colinéarité de deux vecteurs reste valide, etc.
Donc ici, aucun concept nouveau, juste une extension de vos connaissances.
Caractérisation d’un vecteur et propriétés
Soit \(A\) et \(B\) deux points distincts de l’espace.
Le vecteur \(\overrightarrow {AB} \) se caractérise par son sens, sa direction qui est celle de la droite \((AB)\) et la distance \(AB\) qui est sa norme, notée \(\| {\overrightarrow {AB} } \|.\)
Les propriétés sont, elles aussi, les mêmes que dans le plan ; notamment la règle du parallélogramme : \(ABDC\) est un parallélogramme si et seulement si \(\overrightarrow {AB} \) = \(\overrightarrow {CD}.\)
De même, deux vecteurs ne sont égaux que s’ils ont même norme, même sens et même direction.
Si les points \(A\) et \(B\) sont confondus, \(\overrightarrow {AB} \) est le vecteur nul qui se note \(\overrightarrow {0} .\)
Pour tout point \(A\) et tout vecteur \(\overrightarrow {u}\) il existe un point \(B\) unique tel que \(\overrightarrow {AB} = \overrightarrow {u}.\) On dit que \(\overrightarrow {AB} \) est un représentant du vecteur \(\overrightarrow {u}.\)
Opérations sur les vecteurs
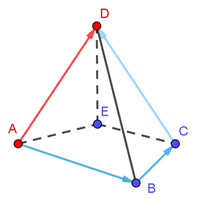
La relation de Chasles s’applique dans l’espace. Illustration ci-dessous où \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD}\) \(=\) \(\overrightarrow {AD} \)
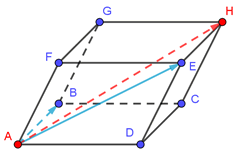
Si vous travaillez sur un parallélogramme, vous pouvez vous servir des égalités entre vecteurs. Dans le parallélépipède ci-dessous, \(\overrightarrow {AB} + \overrightarrow {AE}\) \(=\) \(\overrightarrow {AH} \) puisque \(\overrightarrow {AB}\) \(=\) \(\overrightarrow {EH}.\)
Produit par un réel : soit \(\overrightarrow {u} \) un vecteur non nul et \(k\) un réel non nul. Le vecteur \(k\overrightarrow {u}\) a même direction que \(\overrightarrow {u},\) même sens si \(k > 0\) (et sens contraire si \(k < 0\)) et \(\| {k\overrightarrow {u} } \| = |k|\| {\overrightarrow {u} } \|.\)
Droites dans l’espace
S’il existe un réel non nul \(k\) tel que \(\overrightarrow {v} = k\overrightarrow {u} \) alors les vecteurs \(\overrightarrow {u}\) et \(\overrightarrow {v}\) sont colinéaires.
Soit quatre points de l’espace \(A,\) \(B,\) \(C\) et \(D.\)
Si le vecteur \(\overrightarrow {AB}\) est colinéaire à \(\overrightarrow {BC}\) alors les points \(A,\) \(B\) et \(C\) sont alignés. D’où cette définition d’une droite à partir de deux points distincts \(A\) et \(B\) (qui peut paraître alambiquée) : la droite \((AB)\) est l’ensemble des points \(M\) tels que \(\overrightarrow {AM}\) est colinéaire à \(\overrightarrow {AB}.\)
Si le vecteur \(\overrightarrow {AB}\) est colinéaire à \(\overrightarrow {CD}\) alors les droites \((AB)\) et \((CD)\) sont parallèles.

Combinaisons linéaires
Soit deux réels \(a\) et \(b\) et trois vecteurs de l’espace \(\overrightarrow {u},\) \(\overrightarrow {v}\) et \(\overrightarrow {w}.\)
\(\overrightarrow {w}\) est combinaison linaire de \(\overrightarrow {u}\) et \(\overrightarrow {v}\) si l’on peut écrire \(\overrightarrow {w} = a\overrightarrow {u} + b\overrightarrow {u}.\)
Dans le cas le plus simple, \(a = b = 1.\) C’est ce que nous avons vu plus haut avec le parallélépipède où \(\overrightarrow {AH}\) est combinaison linéaire de \(\overrightarrow {AB}\) et \(\overrightarrow {AE}.\) Notez que l’on peut aussi bien écrire que \(\overrightarrow {AB}\) est combinaison linéaire de \(\overrightarrow {AH}\) et \(\overrightarrow {AE}.\)
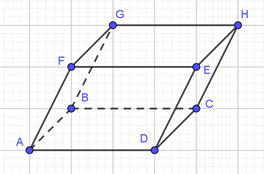
Exemple d’une représentation dans l’espace d’une combinaison linéaire. Reprenons notre parallélépipède préféré.
Positionnons le point \(Z\) tel que :
\(\overrightarrow {AZ}\) \(=\) \(\frac{1}{3}\overrightarrow {BC} + 2\overrightarrow {DE} - 2\overrightarrow {AB}\)
Comme \(\overrightarrow {BC} = \overrightarrow {AD}\) nous pouvons réécrire notre équation ainsi :
\(\overrightarrow {AZ}\) \(=\) \(\frac{1}{3}\overrightarrow {AD} + 2\overrightarrow {DE} + 2\overrightarrow {BA}\)
Donc :
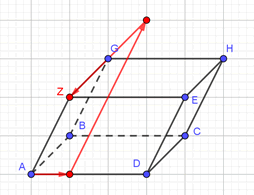
Sur cette représentation on pourrait penser que le point \(Z\) est confondu avec le point \(F\) mais en fait il le cache. N’oublions pas que nous sommes dans l’espace. C’est comme si \(Z\) était entre \(F\) et vous.
