Fonctions circulaires directes
Voici un petit mémo sur les fonctions sinus, cosinus et tangente. En latin, sinus signifie courbé, d'où le mot « sein ». Vous jugerez vous-même si les fonctions trigonométriques ont plus de charme que les autres...
Précisions si vous êtes en première générale, première STI2D ou STL ou terminale générale : considérez cette page comme une ressource pour votre programme de maths. La fonction tangente fait partie des points facultatifs du programme de terminale. En première technologique, zappez la notion de dérivée que vous étudierez un peu plus tard dans l'année.
Fonctions et cercle
Si l’on fait le rapprochement avec le cercle trigonométrique, on devine que les fonctions sinus et cosinus sont périodiques, de période \(2\pi.\) Rappelons ici le cercle dans un repère \((O\,; I ,J)\) afin de mieux mémoriser le lien avec les fonctions.
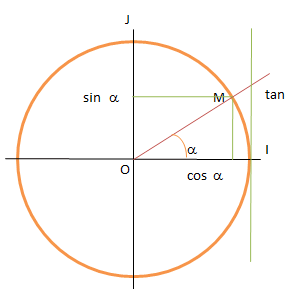
La fonction sinus
C’est une fonction définie et dérivable sur \(\mathbb{R}\), continue et impaire. Sa dérivée est \(\cos(x).\) Une primitive est \(-\cos(x).\) Rappelons qu'une fonction \(f\) est impaire lorsque pour tout \(x\) appartenant à son ensemble de définition \(f(-x) = -f(x).\)
Points remarquables : \(\sin(0) = 0.\) On le lit sur le cercle. Si l’angle est nul, \(M = I\) et donc le sinus, en ordonnée, est égal à zéro. Déplaçons le rayon dans le sens trigonométrique (inverse des aiguilles d’une montre). Si \(M = J,\) cela signifie que la mesure de l'angle est \(\frac{\pi}{2}\) et l'on remarque que \(\sin\left(\frac{\pi}{2}\right) = 1.\) Continuons à déplacer le rayon et notons que \(\sin(\pi) = 0\) puis que \(\sin\left(\frac{\pi}{2}\right) = -1.\) Si l’on fait un tour complet, on voit que \(\sin(2\pi) =0.\)
Par conséquent, ses valeurs sont toujours comprises entre -1 et 1 et \(\sin(x) = \sin(x + 2\pi).\) Il s'ensuit que son ensemble d'étude peut se réduire à l'intervalle \(\left[0\,;\frac{\pi}{2}\right]\) et qu'à l'infini, elle n'admet pas de limite...
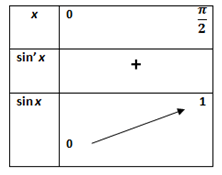
Illustration :
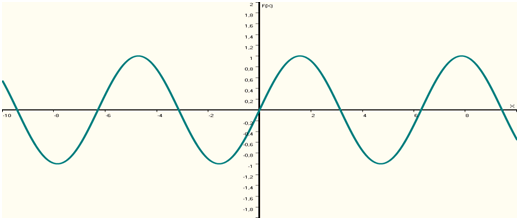
Ce type de fonction est appelé, devinez pourquoi, une sinusoïdale (ou sinusoïde).
Voir les pages d'exercices sur la parité (niveau première) et d'exercices avec fonction sinus (niveau terminale)
La fonction cosinus
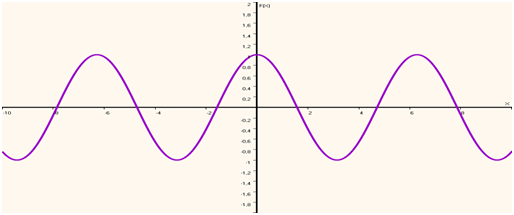
C’est une fonction paire, c'est à dire que \(f(x) = f(-x).\) Comme la fonction sinus, elle est définie, continue et dérivable sur \(\mathbb{R}.\) Elle est également bornée, sa période est la même et elle n'admet pas non plus de limite à l'infini. Sa dérivée est \(-\sin(x)\) et une primitive est \(\sin(x).\) Nous vous laissons le soin de faire le lien avec le cercle trigonométrique et d'imaginer le tableau de variation...
La fonction tangente
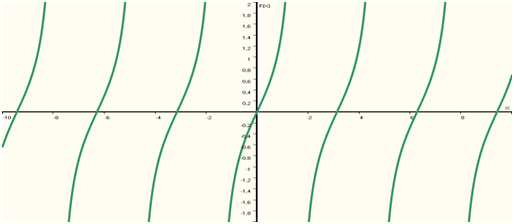
Rappelons que \(\tan(x) = \frac{\sin(x)}{\cos(x)}.\) Donc, la fonction n’est pas continue sur \(\mathbb{R}\) puisqu’elle n’est pas définie chaque fois que \(\cos(x) = 0.\) En revanche, elle part à l’infini lorsque \(\sin(x) = 0.\) D’où la représentation graphique à l'aspect bizarre d'un plan repéré rageusement rayé…
Il s’agit d’une fonction impaire définie lorsque \(x\) est différent de \(\frac{\pi}{2} + k\pi\) (\(k\) étant un entier relatif) et dont la dérivée s’écrit \(1 + \tan^2(x).\)
D'ailleurs, sachant que \(\sin^2(x) + \cos^2(x) = 1,\) il est facile de montrer que cette dérivée peut s'écrire de plusieurs façons :
\(1 + \tan^2(x)\) \(= 1 +\frac{\sin^2(x)}{\cos^2(x)}\) \(= \frac{\cos^2(x) + \sin^2(x)}{\cos^2(x)}\) \(= \frac{1}{\cos^2(x)}\)
Voir également les pages d'exercices de dérivation de fonctions trigonométriques, de dérivées de fonctions de référence et sur les primitives de fonctions trigonométriques.
Prolongements
Notez que toutes ces fonctions sont tantôt convexes tantôt concaves selon les intervalles.
Leurs développements limités au voisinage de zéro figurent en page de développement limité de Mc Laurin (niveau fac).
D'autres fonctions trigonométriques sont issues plus ou moins directement des sinus et cosinus, par exemple les fonctions sécante et cosécante.
Enfin, les fonctions sinus, cosinus et tangente admettent des réciproques sur certains intervalles. Ce sont les fonctions trigonométriques réciproques arc-sinus, arc-cosinus et arc-tangente.
Voir éventuellement les intégrales de Wallis.
