Coût marginal et optimum technique
Depuis des siècles, l’analyse marginale joue les premiers rôles dans les grands blockbusters de l’économie, classiques, keynésiens ou néo-classiques. Mais son apparition dans le monde de l’entreprise se révèle beaucoup plus tardive et timide. A-t-on peur de l’utiliser à contre-emploi, tant son image d’outil théorique lui colle à la peau ?
Problématique
C’est surtout la notion de coût marginal (Cm) qui permet l’utilisation, sinon fréquente du moins appliquée, de l’analyse marginale. Le challenge consiste à évaluer le coût d’une unité produite supplémentaire (en fait, d’accepter ou de refuser une commande).
La détermination du Cm (Incremental cost) est enseignée dans les cadres les plus divers : micro-économie, gestion, maths...
Mathématiquement, le Cm s’évalue comme la dérivée du coût total. L’analyse nécessite donc de déterminer une fonction de coût. Pas forcément évident, d’autant que les contrôleurs de gestion ne montrent pas toujours un amour fou pour les maths. Un exercice de niveau première générale figure en page d'exercice sur fonctions de coût.
Faisons connaissance avec le Cm à travers un exemple. Il s’agit d’un exercice de mathématiques de niveau terminale. Cette présentation théorique est également celle de bon nombre de manuels d’économie (mais ceux-ci exposent rarement des exemples chiffrés).
Exemple
Une fonction \(CT\) de coût total exprime l’ensemble des charges affectées à un produit en fonction d’une quantité non nulle \(x\) de tonnes fabriquées. Soit \(CT(x)\) \(=\) \(x^3 - 2x^2 + 10x + 150.\)
Les fonctions de coût prennent souvent la forme d’une fonction polynomiale du troisième degré (voir le direct costing).
Première question : calculer les expressions des fonctions de coût unitaire (ou moyen) \(CM\) et de coût marginal \(Cm\) puis les représenter graphiquement. Vérifier que les courbes se croisent là où le coût moyen est le plus faible. En préciser les coordonnées.
Première réponse : la fonction de coût moyen est tout simplement celle du coût total divisée par la quantité. Donc, \(CM\) \(=\) \(x^2 - 2x + 10 + \frac{150}{x}.\)
La fonction de coût marginal étant la dérivée de \(CT,\) on obtient \(Cm(x) = 3x^2 - 4x + 10.\) Précisons que la dérivée ne permet qu'une approximation affine. Par exemple, le coût de la sixième tonne s'établit à \(CT(6) - CT(5)\) \(=\) \(354 - 275\) \(=\) \(79\) mais si l'on calcule \(Cm(5)\) on obtient 65 (bien sûr, l'écart serait moins important si la production était calculée au kg près...).
Il est normal d’observer des fonctions de coûts unitaires (moyen ou marginal) décroissantes puis croissantes (donc convexes). Décroissantes parce que les coûts fixes sont rentabilisés au fur et à mesure que la production augmente puis croissantes parce qu’au-delà d'un certain niveau de production celle-ci devient de plus en plus coûteuse (heures supplémentaires, appel à des sous-traitants, etc.).
Réalisation sur http://grapheur.cours-de-math.eu/
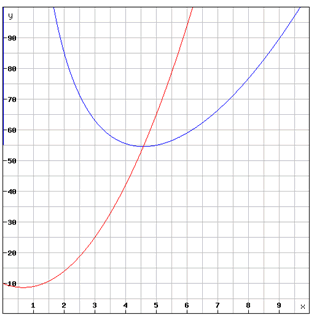
La courbe représentative de \(CM\) est bleue et celle de \(Cm\) est rouge. Et l’on vérifie bien que c’est lorsqu’il est égal au coût marginal que le coût moyen est au plus bas. Ce niveau de production est appelé optimum technique. Tant qu’une tonne supplémentaire est moins coûteuse que la moyenne, il est évident que sa production implique un coût unitaire globalement plus avantageux. Mais au-delà de l’optimum technique, les tonnes produites à des coûts de plus en plus élevés se traduisent par un coût unitaire moyen nécessairement croissant (le graphe est simple à comprendre si l’on explique l’évolution de la courbe bleue par celle de la rouge).
Dans cet exaltant dessein de définir l’optimum technique, on peut choisir entre au moins deux techniques simples. Soit on égalise les expressions des deux fonctions, soit on dérive \(CM\) pour savoir en quel point elle s’annule. Cette deuxième technique nous semble plus rapide à mettre en oeuvre…
\(CM’(x) = 2x - 2 - \frac{150}{x^2}.\) Et aucun moyen algébrique simple de résoudre \(CM’(x) = 0.\) Toutefois, comme cette fonction est continue et strictement croissante entre moins et plus l’infini, le théorème de la bijection (des valeurs intermédiaires) permet d’affirmer qu’il existe UNE solution. Avec une calculatrice, on trouve 4,58.
Pour connaître le coût unitaire (moyen ou marginal), nous calculons \(CM(4,58)\) ou \(Cm(4,58),\) au choix puisque ces coûts sont égaux à ce niveau de production. Il s'avère que le coût s’établit à 54,6 unités monétaires.
Deuxième question : représenter la courbe du coût total. Tracer la tangente au point d’abscisse 4,58 et montrer que le coût moyen est égal au coefficient directeur de cette dernière.
Deuxième réponse : établissons d’abord l’équation de cette tangente. Vous connaissez la formule, soit \(y = CT(4,58) + CT’(4,58)(x - 4,58).\) Passons les détails, nous arrivons à \(y = 54,6x.\) Bien sûr, ce n’est pas un hasard si l’on retrouve ce bon vieux coût marginal de 54,6 en raison de l'équivalence entre nombre dérivé et coefficient directeur de la tangente.
Pour varier les présentations, le deuxième graphe avec été réalisé avec Sine qua non.
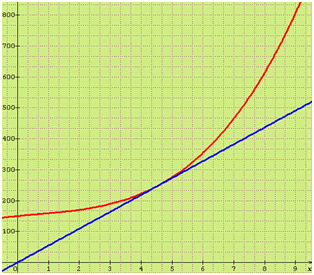
Ce que l’on découvre ici est une deuxième façon de déterminer l’optimum technique : on trace la courbe du coût total puis la seule tangente à cette courbe qui parte de l’origine. Il se trouve que c’est justement la tangente au point d’abscisse 4,58…
Compléments
Une étude sur les coûts est en principe complétée par une étude sur les recettes. La synthèse permet de localiser un optimum économique.
Sur un petit intervalle, on peut utiliser une approximation de la courbe représentative d'une fonction par une droite (voir la reprise de cet exemple en page d'approximation affine).
