Fonctions polynomiales du troisième degré
Niveau de cette page : premières technologiques.
Si vous lisez cette page, vous connaissez déjà la fonction cube. Sa représentation graphique est une cubique (ce terme n'est pas au programme des premières technologiques). Nous allons nous intéresser ci-dessous à cette courbe. Mais auparavant, apportons une précision sur la notation.
Notation
Soit l'équation \(x^3 = c.\) Alors \(x\) est appelée racine cubique de \(c\). Par exemple, \(2 × 2 × 2 = 8\) donc 2 est la racine cubique de 8.

La solution est unique (contrairement à une équation de type \(x^2 = b\)).
Une première notation est \(c^{\frac{1}{3}}.\) Si vous vous souvenez qu'une racine carrée équivaut à une puissance \(\frac{1}{2},\) vous n'êtes pas dépaysé.
Une autre façon est de noter \(\sqrt[3]{c}.\) Ainsi, \(\sqrt[3]{8} = 2.\)
Fonction polynôme de degré 3
Une fonction polynôme de degré 3 est de la forme \(x \mapsto ax^3 + bx^2 + cx + d\) avec \(a ≠ 0.\)
Soit par exemple la fonction \(f\) définie par \(f(x) = 2x^3 + \frac{x}{2} - 1.\) Nous avons \(a = 2,\) \(b = 0,\) \(c = \frac{1}{2}\) et \(d = -1.\)
Représentations graphiques
Soit une fonction de type \(x \mapsto a{x^3}\)
Dans ce cas, la courbe représentative passe par l'origine du repère. Elle ressemble à la courbe qui représente la fonction cube, en plus resserrée si \(a > 0\), plus évasée si \(0 < a < 1\) et inversée si \(a < 0.\)
Ci-dessous, plusieurs courbes ont été tracées avec GeoGebra, la fonction cube figurant en rouge. Remarquez qu'elle passe bien par le point de coordonnées \((2\, ;8)\) puisque, nous l'avons vu, le cube de 2 est 8.
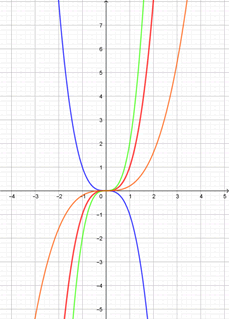
La bleue représente la fonction telle que \(x\mapsto -x^3.\) La verte représente la fonction telle que \(x \mapsto 2x^3\) et la orange représente \(x \mapsto 0,2x^3.\)
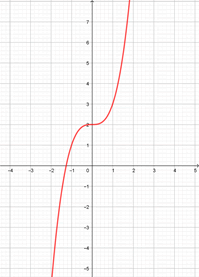
Soit à présent une fonction de type \(x\mapsto ax^3 + d.\) Si l'on ajoute une constante \(d\) à notre fonction, on observe une translation verticale. La courbe ci-dessous représente la fonction \(f\) définie par \(f(x) = x^3 + 2.\) Comme les précédentes, elle admet un centre de symétrie mais pas sur l'origine (en l'occurrence, sur le point de coordonnées \((2\, ;0)\)).
Fonctions de type \(x \mapsto a(x - x_1)(x - x_2)(x - x_3)\)
Une fonction du troisième degré peut parfois être s'écrire sous une forme factorisée : \(x \mapsto a(x - x_1)(x - x_2) )(x - x_3).\)
\(x_1\), \(x_2\) et \(x_3\) sont les racines de la fonction. Ce sont les abscisses des trois points d'intersection entre la courbe et l'axe des abscisses.
Toutes les fonctions du troisième degré ne peuvent pas s'écrire ainsi. La preuve, aucune des courbes ci-dessus ne croise trois fois l'axe des abscisses.
Attention, ces racines sont des réels, éventuellement inférieurs à zéro : il n'y a pas obligatoirement de signe négatif entre \(x\) et la racine !
Le coefficient \(a\) a les mêmes propriétés que dans les configurations plus simples. S'il est négatif, la courbe est inversée.
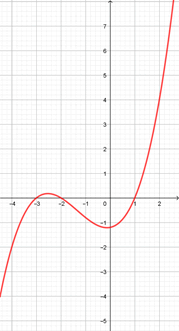
La courbe ci-dessous représente une fonction \(f\) définie par \(f(x)\) \(= 0,2(x - 1)(x + 2)(x + 3).\) Vous remarquez qu'elle zigzague. Les racines de \(f\) sont 1, -2 et -3. On le constate sur la courbe qui traverse l'axe des abscisses en 1, -2 et -3.
Exercice
Reprendre la courbe ci-dessus pour déterminer \(f(2),\) puis vérifier par le calcul.
Corrigé : la courbe semble passer par le point de coordonnées \((2\, ;4).\)
Vérification : \(0,2(2 - 1)(2 + 2)(2 + 3)\) \(= 0,2 × 20 = 4.\)
Voir aussi le second problème de la page sur les problèmes avec fonctions de degrés 2 et 3.
