Fonctions de 2 variables et surfaces avec Excel
Ceci est une introduction aux fonctions de deux variables. Deux, c’est sans doute peu pour modéliser un phénomène, économique ou autre, mais ce n’est déjà pas si mal pour appréhender des situations aussi diverses que, par exemple, les fonctions de production ou la théorie du portefeuille.

Aspects techniques
Ainsi, pour tout couple \((x\,;y)\) on associe un réel \(z.\) Donc \(z = f(x\,;y).\) Graphiquement, \(x\) est l’abscisse (habituellement situé sur l’axe qui semble venir vers nous), \(y\) est l’ordonnée (axe horizontal) et \(z\) est la cote (axe vertical).
Un tel espace permet par exemple de représenter une sphère de centre \((a\,; b\, ;c)\) et de rayon \(r\) :
\((x - a)^2 + (y - b)^2 + (z - c)^2\) \(= r^2\)
Bien entendu, toutes les recherches habituellement menées sur les fonctions d’une variable (et même d'autres) sont effectuées sur les fonctions de deux variables afin d’en connaître toutes les caractéristiques : détermination du domaine de définition, continuité, limites, dérivation, etc. Trois fois hélas, nous n’évoquerons pas ces aspects sur cette page introductive essentiellement consacrée aux représentations graphiques.
Chacun sait depuis sa plus tendre enfance que la représentation d’une fonction d’une variable est une courbe dans le plan. Celle d’une fonction de deux variables est quant à elle une surface courbe dans l’espace.
Quelques logiciels bienveillants nous permettent de tracer sans difficulté ces surfaces, au premier rang desquels Excel.
Cette page détaille le tracé d’une surface à partir d’un exemple.
Soit une surface \(S\) d’équation \(z = y × \ln x,\) où \(x\) appartient à l’intervalle \([0,5\,;5]\) et \(y\) appartient à \([-3\,; 5].\) C’est à partir de cette fonction que diverses questions avaient été posées à l’épreuve de juin 2008 du bac ES spécialité maths en Asie mais le sujet ne sera pas traité ici.
Pour reproduire \(S\) (qui en l’occurrence figurait en annexe de l’énoncé) il faut, avec Excel, créer un tableau.
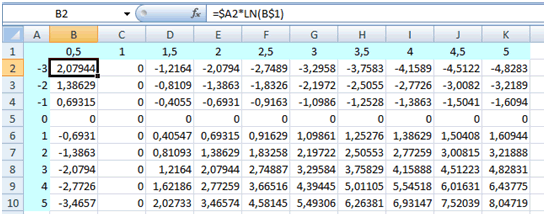
La fonction LN qui paraît dans la barre de formule signifie « logarithme népérien ». Les abscisses pour lesquelles une valeur a été calculée figurent sur la ligne 1 et les ordonnées apparaissent en colonne A.
Représentations graphiques
Il faut ensuite sélectionner toutes les cellules, de A1 à K10, puis dans le menu d’insertion choisir parmi les « autres graphiques » une surface. On obtient un graphique brut qui ressemble à ceci :
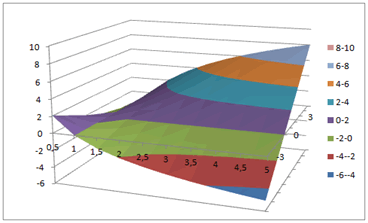
Ce laideron doit subir quelques retouches pour ressembler à celui qui figurait en annexe du sujet du bac : sélection de l’axe des cotes (changer les options d’axe), dans « sélectionner les données » inverser les lignes et les colonnes, demander un ordre inverse pour l’axe horizontal (petite curiosité de cet exercice), tourner l’espace dans « rotation 3D », ajouter des quadrillages secondaires, etc. Et voilà le travail :
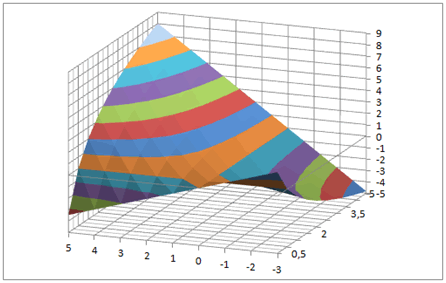
Pour information, un autre type de graphique proposé par Excel produit la même surface mais vue de dessus :
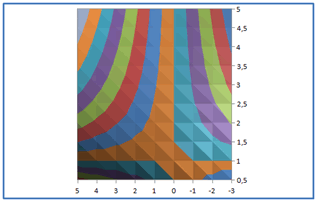
Ces représentations montrent, entre les couleurs, des courbes de niveau. Il s'agit de parties de \(\mathbb{R}^2\) qui vérifient \(f(x\,;y) = k,\) \(k\) étant une constante.
L’une des questions de l’épreuve consistait à représenter l’intersection de \(S\) avec le plan d’équation \(y = 2.\) Dès lors qu’il existe une contrainte sur \(y\) (ou sur \(x\)), on perd une dimension. Le dessin est donc le tracé d'une courbe d’équation \(z = 2ln x.\) Avec Excel, il est particulièrement simple de transformer une énigme du bac en simple formalité. Il suffit pour celà de sélectionner les lignes 1 et 7 (cette dernière correspond à \(y = 2\)) pour obtenir, après un léger lifting…