Régression simple sur tendance exponentielle
Dans les problématiques des entreprises et organisations publiques, la régression est généralement employée sur les séries temporelles, dans une démarche prévisionnelle. Le challenge consiste à trouver l'expression de la fonction qui synthétise au mieux une progression selon la forme du nuage de points représentatif des observations, puis de poursuivre la courbe de tendance sur l'avenir. Sur cette page est présenté un modèle d'ajustement non linéaire susceptible de résumer plusieurs configurations de nuages, la régression sur tendance exponentielle.
Diverses situations
En premier lieu, le modèle peut s'appliquer à des progressions explosives. Rarissime cas de figure et pour cause... L'évolution exponentielle d'un phénomène économique se retourne nécessairement un jour ou l'autre !
La fonction exponentielle permet aussi de formaliser des décroissances ou au contraire des augmentations très importantes qui se stabilisent dans de courts délais (la courbe tend vers une asymptote horizontale), sur les modèles \(e^{-t}\) ou \(-e^{-t}.\)
Alors qu’une tendance linéaire s’applique le plus souvent à des périodes courtes, l’exponentielle se situe dans un cadre de moyen terme. Son expression s’écrit de plusieurs façons dont la plus simple est \(y = b \alpha^t\), avec \( \alpha = e^a.\) Ne pas confondre avec la fonction puissance dont la forme est \(y = bt^a.\)
Mise en pratique
L'équation de la courbe de régression par logiciel ou calculatrice peut être déterminée de deux façons. La première consiste à utiliser les logarithmes des données puis à réaliser une régression linéaire. Cette technique se trouve abondamment dans les annales de mathématiques du bac ES (elle n'est plus au programme depuis l'année 2012-2013). Non détaillée sur ce site, elle est utilisée dans un cadre assez proche en page régression sur tendance logarithmique (le changement de variable s'effectue alors par les exponentielles et non par les logarithmes). L'autre moyen est bien sûr de chercher directement l'équation de la courbe. Une simple calculatrice telle que celles utilisées par les lycéens est d'ailleurs capable de la fournir.
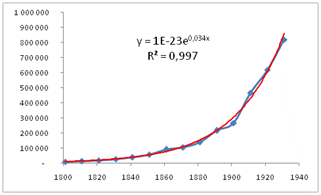
À titre d’exemple, l’évolution de la population montréalaise entre 1801 et 1931 est indiquée ci-dessous (source : ville de Montréal).

On reconnaît du premier coup d’œil l’évolution exponentielle. Avec Excel, on ajoute la courbe de tendance par un clic droit sur la courbe des observations, puis « ajouter une courbe de tendance » et l’option « courbe exponentielle », avec ajout de l’équation et du \(R^2\). Ce dernier montre d’ailleurs un excellent ajustement. Mais on peut regretter l’imprécision de l’équation qui en empêche toute utilisation ! (pour info, les valeurs des années ont été reprises telles quelles et non en posant \(t = 1, 2, 3…).\)
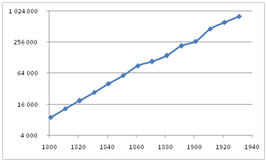
Mécaniquement, si l’on trace la courbe sur un repère logarithmique en \(y\), les données sont proches d’une droite.
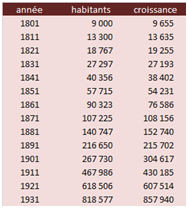
Fort obligeamment, Excel nous restitue les principales informations utiles grâce à la fonction LOGREG. Le tableau ci-dessous reprend les observations dans la colonne « habitants » et les valeurs calculées dans la colonne croissance, obtenue tout simplement avec la fonction CROISSANCE (sélection de toute la troisième colonne, indiquez la plage de la deuxième colonne dans la formule puis Ctrl + Maj + Entrée).
LOGREG s’utilise exactement comme DROITEREG et nous permet d’admirer ce magnifique résultat :
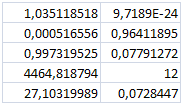
La première ligne nous indique un taux de croissance de \(3,512\% \) par an. L’équation de la courbe peut se lire ainsi : population =\(9,7189 \times {10^{ - 24}} \times {(1 + 3,512\% )^{{\rm{année}}}}.\)
Les prévisions peuvent être réalisées avec cette équation. La deuxième ligne est celle des écarts-types des paramètres de l’équation. La troisième ligne nous donne cet excellent \(R^2\) et l'estimation de l'écart-type des erreurs, la quatrième ligne nous indique la valeur du \(F\) (non moins excellente) et le nombre de degrés de liberté. La dernière ligne nous restitue le somme des carrés et la somme des carrés des résidus.
Ces informations sur la qualité de la régression nous permettent de comparer, le cas échéant, ce modèle avec d’autres prévisions.
Ce charmant exemple est repris en page de test des séquences. Le choix du modèle y est heureusement conforté.
N’oublions pas que dans la réalité, hormis certains cas de rendements financiers, une évolution exponentielle temporelle finit toujours pas se transformer en autre chose (courbe de type logistique, courbe de Gompertz ou… krach !).
