Graphiques dans repère semi-logarithmique
Imaginez notre monde actuel privé de cette invention géniale que fut celle des représentations graphiques. Impossible ! Et surtout, impossible d’imaginer tout ce qui n’aurait physiquement jamais vu le jour sans cette aide, fondamentale pour toute science…
Hélas, même les types de graphiques les plus courants ont leurs écueils.
Utilité
Ainsi, une courbe indique un niveau. Habituellement, on la présente dans un repère arithmétique (ou linéaire), l’écart de graduation entre 0 et 1 étant par exemple le même qu’entre 100 et 101 (voir la page sur la géométrie analytique). Mais les variations peuvent ne pas être très visibles. Pour les mettre en valeur, il faut alors utiliser un repère semi-logarithmique.
L’écartement entre les valeurs des ordonnées ne suit pas une règle arithmétique mais correspond aux logarithmes népériens ou décimaux. On parle de repère semi-logarithmique si un seul axe bénéficie de cette transformation. On en trouve parfois dans des revues ou sur le web mais malheureusement, il est rarement précisé quel type de logarithme est utilisé (le décimal est le plus fréquent). Dans la mesure où un logarithme est strictement positif, l’axe ne descend pas au-dessous de zéro.
Les courbes ne sont pas les seuls types de graphique à s’accommoder de l’échelle logarithmique. Un nuage de points ou un graphique en barres sont tout à fait susceptibles d’être présentés ainsi.
Bien que moins fréquentes qu’en physique ou en chimie, les représentations sur repère semi-logarithmique ne sont pas rares en économie, et particulièrement dans le domaine boursier (voir l'exemple 2 ci-dessous).
Parfois, c'est l'axe des abscisses qui a avantage à se présenter sur une échelle logarithmique (voir la matrice du BCG).
Comment ça marche ?
Voici la courbe représentative de la fonction logarithme décimal (réalisation sur sine qua non) :
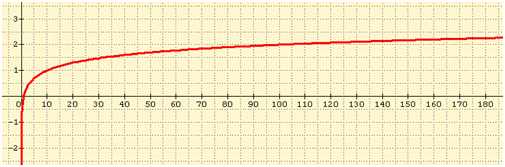
À la place des valeurs indiquées sur l’axe des ordonnées, on indique celle qui est lue sur la courbe. Donc, on remplace 1 par 10, 2 par 100, etc.
Exemple 1 : comparaison de deux évolutions
Il est plus aisé de comparer graphiquement des variations avec cette échelle puisqu’un écartement de \(x\%\) sur l’axe des ordonnées reste le même quel que soit le niveau de \(y.\) Ainsi, sur une échelle arithmétique, la distance entre 40 et 80 est deux fois plus grande qu’entre 20 et 40 alors que sur une échelle logarithmique elles sont égales (\(+ 100\,%\) dans les deux cas) :
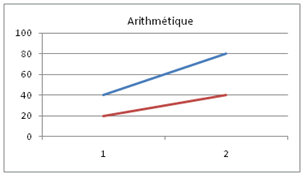
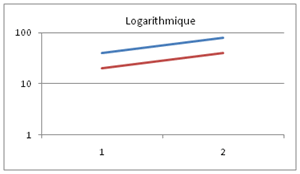
Ces graphiques ont été réalisés avec Excel. Pour le deuxième, il suffit de sélectionner l’axe des ordonnées, clic droit pour faire apparaître le menu contextuel puis mise en forme de l’axe… Dans le menu qui apparaît, on coche la case échelle logarithmique. On remarque qu’Excel nous donne le choix de n’importe quelle base. En l’occurrence, on laisse 10 qui est la valeur par défaut. Notez qu'Excel permet aussi de graduer l'axe des abscisses en échelle logarithmique.
Exemple 2 : gagnez de l’argent grâce aux logarithmes !
Une évolution longue montre souvent de fortes disparités. L’évolution du PIB d’un pays riche entre le dix-neuvième siècle et la période actuelle ne permettrait pas de discerner les mouvements du début de période, écrasés par l’échelle. Mais ce sont surtout les évolutions observées à la bourse qui donnent lieu à une utilisation très classique des échelles logarithmiques. Pourtant, l’analyse technique privilégie généralement l’échelle arithmétique…

Voici par exemple l’évolution du prix de l’action Altran Technologie sur une longue période (source Boursorama). Sur l’échelle logarithmique, la bulle spéculative qui a existé sur ce type de valeur autour de 2000 apparaît très clairement. En revanche, on ne distingue pas très bien les soubresauts ni avant 1998 ni après 2002.
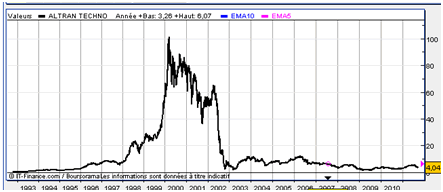
Si l’on coche l’option Echelle Log, on obtient quelque chose de très différent :
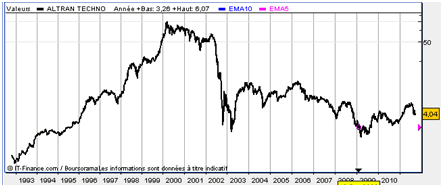
Il apparaît que la période la plus lucrative pour un investisseur a été courant 2003, soit après l’éclatement de la bulle, et non fin 99 début 2000, ce qui n’était pas évident à la vue du graphique précédent ! En près de neuf mois, le prix de l’action a été multiplié par 4,8 alors que la performance plus « visible » fut une multiplication par 4,1 sur une période à peu près identique avant le plus haut historique. Moralité : il vaut mieux jouer le rebond, plus lucratif et moins risqué (nous vous laissons vérifier si cette observation est valable sur d’autres titres) ...
Exemples statistiques
Voir pages régression sur tendance exponentielle, séries chronologiques.
