Droites concourantes
Cette page est consacrée aux lieux de rendez-vous des droites. Il s’agit de points vers lesquels elles convergent de fort loin… Difficiles à trouver ? Non, le niveau de difficulté de cette page est celui d'une première générale. Les familles de droites ne sont pas expressément au programme mais il n'est pas rare de devoir plancher sur un exercice de ce type. Si vous êtes en première, c'est surtout la fin de la page qui vous intéressera.
Géométrie dans le plan
Rappel. Plusieurs droites distinctes sont concourantes si elles sont sécantes en un point commun.
Un petit exercice rapide pour introduire le sujet. Nous sommes en présence d’un bon vieux rectangle \(ABCD.\)
- \(\overrightarrow {AE} = \frac{1}{4} \overrightarrow {AB}\)
- \(\overrightarrow {DF} = \frac{3}{4} \overrightarrow {DC}\)
- \(\overrightarrow {AG} = \frac{1}{2} \overrightarrow {AB}\)
- \(\overrightarrow {DH} = \frac{1}{2} \overrightarrow {DC}\)
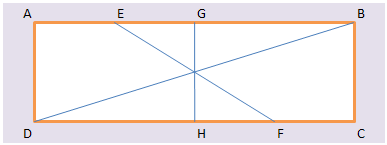
Il faut montrer que les droites \((EF),\) \((GH)\) et \((DB)\) sont concourantes.
Que notre figure soit un rectangle ou un parallélogramme quelconque ne change rien à l’affaire. Le milieu de \([BD]\) en est le centre de gravité, ainsi que le milieu de \([GH].\) Donc, \((BD)\) et \((CH)\) sont concourantes en ce point.
On démontre ensuite que \(EGFH\) est un parallélogramme puisque le vecteur \(\overrightarrow {EG}\) est égal au quart de \(\overrightarrow {AB}\) et idem pour \(\overrightarrow {HF},\) les deux étant de surcroît parallèles et donc que le milieu de \([GH]\) est aussi le milieu de \([EF].\) Nos trois droites se croisent bien au même endroit.
Il est évident que si deux droites non parallèles sont concourantes, cette propriété n’est plus obligatoirement vérifiée s’il y en a trois.
Note : les propriétés de l'homothétie peuvent être mises à contribution pour démontrer que trois droites sont sécantes en un seul point.
Géométrie dans l’espace
Il existe toujours plusieurs possibilités pour montrer que des droites sont concourantes. On se passera d’exemple. Une famille de droites formées par les arêtes des faces latérales d’une pyramide est mentalement visualisable par le commun des mortels (elles se rejoignent au sommet).

Familles de droites
On se situe maintenant dans un plan muni d'un repère, à deux dimensions pour simplifier.
Là aussi, c’est à travers un exercice que l’on appréhendera une étonnante propriété.
Soit un réel \(m\) auquel est associée une famille de droites.
\((m - 2)y = (m + 4)x + m + 1\)
Ce qui est étonnant, c’est que quelle que soit la valeur de \(m,\) toutes les droites de la famille passeront par le même point (bon, ce n'est pas de la magie non plus, c'est une propriété qui se démontre).
Prenons quatre valeurs. Si \(m = 0,\) nous avons la droite d'équation réduite \(y = -2x - 0,5.\) Si \(m = 1,\) alors \(y = -5x - 2.\) Si \(m = -2,\) \(y = -0,5x + 0,25\) et si \(m = 9,\) \(y = \frac{13}{7}x + \frac{10}{7}.\)
Les droites représentatives sont tracées avec le logiciel Sine Qua Non :
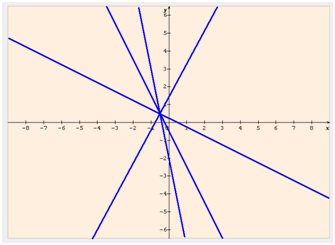
Et où se situe \(A,\) point de rencontre familial ?
Facile, il suffit de retenir les expressions de deux droites et de poser un système de deux équations à deux inconnues. Prenons les deux premières.
\(\left\{ {\begin{array}{*{20}{c}} {y = - 2x - 0,5}\\ {y = - 5x - 2} \end{array}} \right.\)
On trouve \(x = -0,5\) puis \(y = 0,5.\) Ce fameux point \(A\) a donc pour coordonnées \((-0,5\,; 0,5).\)
Vérifions que \(A\) fait TOUJOURS partie de la famille. Dans l'expression générale, on remplace \(x\) par -0,5 et \(y\) par 0,5. Ce qui nous donne :
\((m - 2) \times 0,5 = (m + 4) \times (-0,5) + m + 1.\)
En simplifiant l'égalité, on obtient \(0,5m - 1 = 0,5m - 1.\) Quel que soit \(m,\) c’est OK.
Reprenons à présent l'exercice en utilisant l'équation cartésienne de la droite, ce qui s'inscrit mieux dans l'actuel programme de première générale.
\(-(m + 4)x + (m - 2)y - m - 1 = 0\)
C'est bien une équation de droite car les coefficients de \(x\) et \(y,\) respectivement \((-m - 4)\) et \((m - 2),\) ne peuvent pas s'annuler simultanément.
\( -mx - 4x + my - 2y - m - 1 = 0\)
\(\Leftrightarrow m(-x + y - 1) - 4x - 2y - 1 = 0\)
Si toutes les droites qui vérifient cette égalité ont un point commun, alors il ne doit pas subsister de \(m,\) c'est-à-dire que son coefficient \(-x + y - 1\) doit être nul. Par ailleurs, ce qui reste de l'équation de droite doit bien sûr se vérifier. D'où le système suivant...
\(\left\{ {\begin{array}{*{20}{c}} { - x + y - 1 = 0}\\ { - 4x - 2y - 1 = 0} \end{array}} \right.\)
La résolution par substitution est assez rapide.
\(\left\{ {\begin{array}{*{20}{c}} {y = x + 1}\\ { - 4x - 2(x + 1) - 1 = 0} \end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = x + 1}\\ { - 6x - 3 = 0} \end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = x + 1}\\ {x = - 0,5} \end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = 0,5}\\ {x = - 0,5} \end{array}} \right.\)
Nous retrouvons bien notre point de coordonnées \((-0,5\,; 0,5)\) où concourent toutes les droites de type \((m - 2)y\) \(= (m + 4)x + m + 1.\)
Pour aller plus loin, l'exercice sur une famille de paraboles vous tend les bras...
