Transformations dans le plan et le plan complexe
Cette page donne un aperçu de quelques transformations géométriques. Le vocabulaire utilisé est habituel lorsqu’on utilise des logiciels de retouche photo. Pour une approche plus détaillée des notions, mais se situant à un niveau d'étude inférieur (collège), voir les transformations de figures.
Notez que cette page servait de ressource pour un ancien programme de maths de lycée. Aujourd'hui, les transformations ne sont plus étudiées dans le plan complexe mais elles sont enseignées avec les matrices en terminale maths expertes. Voir la page sur les matrices et la géométrie.
Une transformation est une application bijective dans le plan (ou l'espace), une transformation réciproque permettant de revenir au point de départ. Il en existe de plusieurs types.
La translation
C'est le glissement d’une figure sans pivotement. Ce type de transformation existe en géométrie mais s'applique aussi aux courbes représentatives de fonctions dans le plan (ou l'espace). Par exemple une translation de courbe verticale correspond à l'ajout d'une constante à l’expression de la fonction.
La notion de vecteur est inséparable de celle de translation. Ainsi, la translation d’une figure s’opère en appliquant un même vecteur à tous ses points (Cf. l'initiation aux vecteurs). On obtient une figure identique (mêmes longueurs, mêmes aires) mais située ailleurs dans le plan. C’est un simple copier-coller.
Dans le plan complexe, l’application qui pour tout point d’affixe \(z\) associe un autre point d’affixe \(z'\) en lui ajoutant le complexe \(a\) est la translation de vecteur \(\overrightarrow{u}\) d’affixe \(a.\)
Exemple : la transformation qui à tout point \(M\) d’affixe \(z\) associe un point \(M’\) d’affixe \(z’ = z + 1 + 3i\) est une translation de vecteur \(\overrightarrow{v}\) d’affixe \(a = 1 + 3i.\)
La réflexion
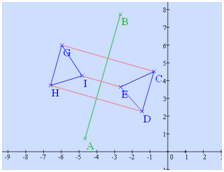
De même qu’un objet se reflète dans l’eau, son image étant inversée, une figure ou un point se reflète dans le plan par rapport à une droite (axe de symétrie). Cette dernière se trouve donc toujours à mi-chemin entre un point et son image. Exemple ci-dessous avec TracenPoche Sésamath. On voit la réflexion du triangle \(HIJ\) par rapport à un axe \(AB.\) Les segments de construction, en rouge, sont à angle droit de \((AB).\)

La rotation
Nul besoin d'être un derviche tourneur pour en comprendre le principe. La figure pivote autour d’un point appelé centre de rotation. Là encore, distances et aires sont conservées. Si l’on travaille avec des nombres complexes, on doit se tourner vers leur forme exponentielle. La rotation nécessite un centre \(Ω\) d’affixe \(ω\) et un angle \(θ.\) Si \(z\) est l’affixe du point auquel on applique la rotation (pour se retrouver sur un point d’affixe \(z’\)), on obtient :
\(z' - \omega = e^{i \theta}(z - \omega )\)
Certaines rotations sont à connaître, notamment les quarts de tour :
\(e^{i \frac{\pi}{2}} = i\) et \(e^{-i \frac{\pi}{2}} = -i\)
L’exemple suivant est extrait d’une épreuve du bac S (Amérique du nord 2008). Les épisodes précédents se trouvent en page de complexes et calcul vectoriel mais en voici le résumé. Nous avons trois points \(A,\) \(M\) et \(B\) d’affixes respectives \(2 +i,\) \(\frac{3}{5} + \frac{6}{5}i\) et 1. Enfin, une question non traitée sur cette page fait état d’un cercle \((γ\,’)\) de diamètre \([AB].\)
- On désigne par \(M’\) l’image du point \(M\) par la rotation de centre \(B\) et d’angle \(- \frac{\pi}{2}.\) Déterminer l’affixe du point \(M’\) et montrer que le point \(M’\) appartient au cercle \((γ\,’).\)
Pour trouver l’affixe de \(M’,\) appliquons d’abord la formule.
\(z' - z_B\) \(=\) \(e^{-i \frac{\pi}{2}}(z - z_B)\)
Donc \(z’\) \(=\) \(1 - –i(z - 1)\) \(=\) \(-iz + i + 1\) (voir la formule du quart de tour). Avec la valeur de \(z\)...
\(z'\) \(=\) \(-i(\frac{3}{5} + i \frac{6}{5}) + i + 1\) \(=\) \(\frac{11}{5} + \frac{2}{5}i\)
Pour répondre au dernier point, il faut en connaître davantage sur le cercle. Pas de problème pour situer le centre, au milieu de \([AB].\) On trouve \(ω = \frac{3}{2} + \frac{i}{2}.\)
Quel est le rayon du cercle ? Simple calcul de distance (voir la page complexes et calcul vectoriel).
\(\frac{AB}{2}\) \(=\) \(\frac{|1-2-i|}{2}\) \(=\) \(\frac{\sqrt{(-1)^2+(-1)^2}}{2}\) \(=\) \(\frac{\sqrt{2}}{2}\)
Ainsi, pour montrer que \(M’\) se trouve bien sur le cercle, il faut vérifier que c’est cette distance-ci qui le sépare du centre \(Ω.\) Donc, même type de calcul et nous vous laissons le soin de vérifier qu’on trouve bien la même chose…
L’homothétie
La forme de la figure reste la même mais sa taille change. Deux paramètres définissent la transformation : le point à partir duquel elle s’effectue et le rapport de taille. Ainsi une homothétie \((O\,;k)\) signifie qu’un vecteur \(\overrightarrow {OA}\) doit être multiplié par le réel \(k\) pour obtenir un vecteur \(\overrightarrow {OA'}.\) Tandis que les distances sont multipliées par \(|k|,\) les aires le sont par \(k^2.\)
Le point invariant est celui dont l’image par l’application reste lui-même. Il est unique aussi bien pour l’homothétie que pour la rotation.
Dans l’exemple qui suit, on part d’un résultat observé pour déterminer les deux paramètres de l’homothétie. À tout point \(M\) une application \(f\) associe un point \(M’\) tel que \(\overrightarrow {MM'}\) \(=\) \(a \overrightarrow {MA} + a \overrightarrow {MB}.\)
\(a\) est un réel quelconque. Cherchons les deux paramètres d’une éventuelle homothétie.
Première étape : trouver le point invariant. L’astuce consiste à utiliser le milieu de \([AB].\) En l’occurrence, il n’est pas bien caché puisqu’il n’est autre que \(M.\) En effet, quelle condition doit remplir \(M\) pour être égal à \(M’\) ?
\(M = M'\)
\(\Leftrightarrow a \overrightarrow {MA} + a \overrightarrow {MB} = \overrightarrow {0}\)
Si les vecteurs \(\overrightarrow {MA}\) et \(\overrightarrow {BM}\) sont égaux, c'est que \(M\) est le milieu de \([AB].\)
Seconde étape : envisager \(M’\) pas nécessairement égal à \(M.\) On trouvera alors le rapport d’homothétie \(k\) grâce à la relation de Chasles. Utilisons l’invariant \(I\) (qui n’est pas égal à \(M\) dans toutes les situations, c’est pourquoi on les distinguera) car la comparaison des vecteurs \(\overrightarrow {IM}\) et \(\overrightarrow {IM'}\) est un très bon moyen de mettre à jour le mystérieux \(k.\)
\(\overrightarrow {MM'}\) \(=\) \(\overrightarrow {MI} + \overrightarrow {IM'}\) \(=\) \(a(\overrightarrow {MI} + \overrightarrow {IA}) + a(\overrightarrow {MI} + \overrightarrow {IB})\)
\(\overrightarrow {IM'}\) \(=\) \(a \overrightarrow {MI} + a \overrightarrow {IA} + a \overrightarrow {MI} + a \overrightarrow {IB} - \overrightarrow {MI}\)
Le cas qui nous occupe est assez simple puisque, \(I\) étant le milieu de \([AB],\) la somme de \(\overrightarrow {IA}\) et \(\overrightarrow {IB}\) nous donne le vecteur nul. Après factorisation, on obtient :
\(\overrightarrow {IM'}\) \(=\) \((2a - 1) \overrightarrow {MI} + \overrightarrow {0}\)
\(\overrightarrow {IM'}\) \(=\) \((-2a + 1) \overrightarrow {IM}\)
Le rapport \(k\) s’établit à \(-2a + 1.\)
Terminons cette brève présentation par l’homothétie dans le plan complexe. Ici, l’homothétie de centre \(Ω,\) d’affixe \(ω\) et de rapport \(k\) est tout simplement \(z’ - ω\) \(=\) \(k(z - ω).\)
