Cercle, disque et tangente au cercle
Bien sûr, il n’est pas question d’être exhaustif sur un sujet aussi vaste que le cercle. Ou la sphère. Même si elle a la taille d'une bulle d'eau gazeuse. Bon, ne nous égarons pas. Cette page se situera au niveau du programme de seconde, agrémenté de quelques notions qui ne vous seront pas toutes utiles mais comme elles sont là, à quémander une petite place dans votre mémoire, accueillez-les avec bienveillance.
Rappelons quelques définitions et propriétés avant d'aborder la notion de tangente au cercle (exercices à l'appui). Voir aussi la page sur l'équation d'un cercle (niveau première générale).
Définitions
Le cercle de centre \(O\) et de rayon \(r\) est l’ensemble des points situés à la même distance \(r\) du point \(O.\)
Le diamètre du cercle est le segment de droite qui passe par le centre \(O\) et dont les bornes sont deux points du cercle. La longueur du diamètre est donc le double de celle du rayon. Vous le savez depuis l'école élémentaire mais là, on s'échauffe.
La longueur du cercle est appelée circonférence. Sa mesure est égale à \(2πr.\) Donc le diamètre multiplié par 3,14 et des poussières (voir la page sur \(\pi\)).
Un arc de cercle est une partie de la circonférence. Une corde est le segment qui relie les deux extrémités de l’arc. La médiatrice de la corde permet de déterminer le milieu de l’arc.
Le disque de centre \(O\) et de rayon \(r\) est l’ensemble des points situés à une distance inférieure ou égale à \(r\) du point \(O\) (le périmètre d’un disque représente donc un cercle). L’aire du disque est égale à \(πr^2.\) De tous les périmètres des figures possibles, celui qui permet d'obtenir une aire maximale est le cercle.
Cercle inscrit
Un cercle inscrit dans un polygone est tangent à tous les côtés de ce polygone (triangle, carré ou autre polygone régulier).
Les bissectrices d’un triangle sont concourantes. Leur point de concours est le centre du cercle inscrit dans ce triangle. Illustration avec GeoGebra :
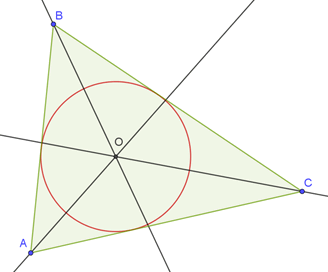
Tangente au cercle
La tangente en un point \(M\) d’un cercle de centre \(O\) est la droite perpendiculaire en \(M\) à \(OM.\) Le point \(M\) est appelé point de contact du cercle et de la tangente.
La tangente ne coupe donc pas le cercle. Elle le « frôle » de façon à n’avoir qu’un seul point en commun avec lui. Ce point \(M\) est le projeté orthogonal du point \(O\) sur la tangente.
Quel est l’intérêt d’introduire en seconde la notion de tangente au cercle ? Il est double : d’une part elle permet de réactiver certaines connaissances, notamment l'indispensable théorème de Pythagore (voir exercice ci-dessous) et d’autre part elle prépare à la notion de tangente à une courbe représentative d’une fonction que l’on étudie en classe de première.

Exercice 1
Soit un cercle \((\mathscr{C})\) de centre \(O.\) Soit \(A\) et \(B\) deux points diamétralement opposés de \((\mathscr{C}).\)
\([AB] = 10\) cm. Soit \(C\) un point du cercle et \(D\) un point de \([OA]\) tel que \(OD = 4\) cm et \(CD = 3\) cm.
Après avoir montré que \(OCD\) est un triangle rectangle, montrer que la tangente de \((\mathscr{C})\) en \(B\) est parallèle à \((CD).\)
Exercice 2
Soit le cercle représenté ci-dessous. \(F\) est l’un de ses points et \(M\) est son milieu.
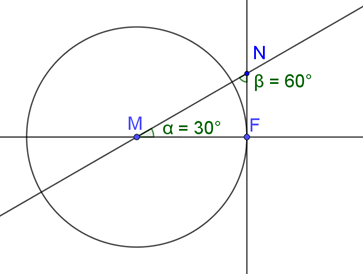
Démontrer que la droite \((NF)\) est tangente au cercle.
Corrigé 1
On peut s’appuyer sur un dessin…
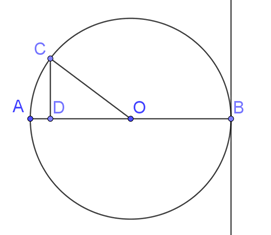
\(OC\) est la longueur du rayon de \((\mathscr{C}),\) soit 5 cm. L’énoncé précise également que \(OD = 4\) cm et \(CD = 3\) cm.
Nous avons \(OC^2 = 25,\) \(OD^2 = 16\) et \(CD^2 = 9.\) Ainsi, \(OC^2 = OD^2 + CD^2.\) D’après la réciproque du théorème de Pythagore, \(OCD\) est un triangle rectangle en \(D.\)
Comme \(OCD\) est rectangle en \(D\) et que \(D\) est un point de \([OA],\) donc de la droite \((AB),\) alors \((CD)\) est perpendiculaire à \((AB).\) La tangente en \(B\) étant perpendiculaire au diamètre \([AB],\) elle est parallèle à toute autre perpendiculaire à \((AB),\) donc à \((CD).\)
Corrigé 2
On sait que le triangle \(MNF\) a un angle \(\widehat M\) mesurant 30° et un angle \(\widehat N\) de 60°. Or, la somme des angles d’un triangle est égale à 180°. Donc l’angle \(\widehat F\) mesure 90°. Ainsi la droite \((NF)\) est perpendiculaire à la droite \((MF).\) On sait que \([MF]\) est un rayon du cercle. Donc \((NF)\) est tangente au cercle.
