Découverte des matrices
Cette page introduit la notion de matrice, avec un peu de vocabulaire et un aperçu des deux opérations les plus simples. La traduction matricielle d’une situation concrète est une démarche souvent retenue pour présenter cet outil mathématique puissant dans l’enseignement de maths expertes en terminale générale.
Nous devons l'invention des matrices au génie britannique du dix-neuvième siècle Arthur Cayley, qui révolutionna plusieurs branches des mathématiques (tout en exerçant la profession d'avocat pour des raisons financières). Il les nomma ainsi par analogie avec les matrices utilisées dans l'imprimerie.
Les applications sont très nombreuses. Si vous êtes en terminale, vous entreverrez quelques applications (chaînes de Markov, transformations du plan...) mais c'est au cours de vos études supérieures que vous mesurerez la puissance de cet outil.
Vocabulaire
Les matrices sont tout simplement des tableaux avec lesquels il est possible de faire des opérations. Elles sont présentées d’une façon un peu différente d’eux, entre parenthèses. Le contenu d’une case de tableau devient un coefficient de matrice (parfois appelé élément).
Comme un tableau, la matrice est rectangulaire. Admettons qu’elle possède \(m\)lignes et \(n\) colonnes. On dit alors qu’elle est d’ordre \((m,n)\) ou de dimensions \(m \times n.\) Si \(m = n,\) nous sommes en présence d’une matrice carrée. Si \(m = 1\) et \(n > 1,\) il s’agit d’une matrice-ligne, également nommée vecteur-ligne (et revoilà les vecteurs là où vous ne les attendiez pas !). Bien sûr si \(n = 1\) et \(m > 1\) il s’agit d’une matrice-colonne ou vecteur-colonne.
Revenons aux coefficients et appelons-les \(a.\) Plus précisément, nommons \(a_{ij}\) le coefficient qui se trouve à l’intersection de la ligne \(i\) et de la colonne \(j\) dans la matrice \(M.\) Le modèle est le suivant :
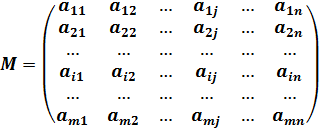
Remarquez que ce système de notation est celui que l’on utilise en statistiques.
Deux matrices \(A\) et \(B\) sont égales si elles sont de même dimension et si chaque coefficient \(a_{ij}\) de \(A\) est égal au coefficient \(b_{ij}\) de \(B.\)
Opérations
La somme : pour additionner (ou soustraire) deux matrices \(A\) et \(B\) entre elles, il faut qu'elles soient de même dimension. Il suffit alors d’additionner chaque coefficient \(a_{ij}\) de \(A\) avec chaque coefficient \(b_{ij}\) de \(B.\)
Exemple :
Soit \(A = \left( {\begin{array}{*{20}{c}} 2&1\\ 0&{ - 5} \end{array}} \right)\) et \(B = \left( {\begin{array}{*{20}{c}} 3&{ - 8}\\ 2&{ - 1} \end{array}} \right)\)
Nous obtenons alors \(A + B = \left( {\begin{array}{*{20}{c}} 5&{ - 7}\\ 2&{ - 6} \end{array}} \right)\)
L'addition de matrices est commutative. \(A + B = B + A.\)
Elle est également associative. \((A + B) + C\) \(=\) \(A + (B + C).\)
Elle admet un élément neutre, la matrice nulle (elle a les mêmes dimensions que la matrice à laquelle elle s'ajoute et elle ne comporte que des zéros).
La multiplication par un scalaire : une matrice \(M\) peut être multipliée (ou divisée) par un réel \(k.\) Il suffit de multiplier chacun de ses coefficients par \(k.\) Voir l’exemple ci-dessous.
Si \(k = -1,\) on obtient la matrice \(-M,\) opposée de \(M.\) Si \(k = 0,\) on obtient la matrice nulle.
Traduction matricielle
La société Matrix possède trois hôtels (Annecy, Lyon et Mâcon). Chacun d’eux dégage des bénéfices dans trois types d’activité : hôtellerie, restauration et soins du corps. Ces bénéfices apparaissent dans le tableau ci-dessous :
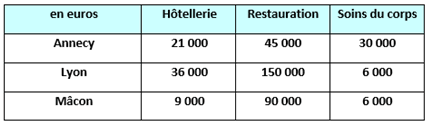
Nous pouvons transcrire ces données dans une matrice carrée :
\(M = \left( {\begin{array}{*{20}{c}} {21000}&{45000}&{30000}\\ {36000}&{150000}&{6000}\\ {9000}&{90000}&{6000} \end{array}} \right)\)
Multiplication par un scalaire : supposons que l’impôt sur les bénéfices soit d’un tiers (\(33,33 \%\)). Nous souhaitons connaître le bénéfice après impôt généré par l’activité de chaque hôtel. Pour cela, multiplions \(M\) par \(\frac{2}{3}\).
\(\frac{2}{3} \times M = \left( {\begin{array}{*{20}{c}}
{14000}&{30000}&{20000}\\
{24000}&{100000}&{4000}\\
{6000}&{60000}&{4000}
\end{array}} \right)\)
Exercice
Dans une réserve africaine s’ébattent joyeusement 290 grands mammifères : 250 éléphants dont 120 mâles, 36 lions dont les deux tiers sont des lionnes et 4 rhinocéros dont une seule femelle. Traduire ces données sous forme matricielle.

Éléments de correction
Plusieurs solutions sont possibles. Nous pouvons présenter les sexes en ligne et les espèces en colonne ou inversement. L’ordre dans lequel apparaissent les uns et les autres peut aussi varier. C’est pourquoi il est préférable de dresser d’abord un tableau avec les intitulés des lignes et des colonnes avant de le traduire sous forme matricielle. Des calculs pourront éventuellement être réalisés à l’aide de cette matrice, quitte à revenir ensuite à la forme tableau, mais ce n’est pas l’objet de cet exercice.
| Éléphants | Lions | Rhinocéros | |
| Mâles | 120 | 12 | 3 |
| Femelles | 130 | 24 | 1 |
Soit \(M\) la matrice correspondante.
\(M = \left( {\begin{array}{*{20}{c}} \begin{array}{l} 120\\ 130 \end{array}&\begin{array}{l} 12\\ 24 \end{array}&\begin{array}{l} 3\\ 1 \end{array} \end{array}} \right)\)
Liens : si vous utilisez une calculatrice TI-83, poursuivez votre découverte des matrices en page de prise en main de la TI pour les matrices. Si c'est une Casio que vous possédez, le mode d'utilisation est en page de puissance d'une matrice. Pour un autre exemple de données concrètes traduites en matrices, voir l'exercice de synthèse issu d'une épreuve du bac ES.
