Introduction aux chaînes de Markov
Le niveau de difficulté de cette page est celui de terminale générale maths expertes.
Ne craignons pas les comparaisons, les chaînes de Markov sont un délicieux dessert de fin d’année. Ce modèle dynamique synthétise en effet plusieurs chapitres découverts au lycée : les probabilités, les matrices, les suites et les graphes. Un régal.
Cadre d'analyse
La chaîne de Markov décrit un processus aléatoire.
Soit \(n \in \mathbb{N}\) et \((X_n)\) une suite de variables aléatoires qui peuvent prendre \(k\) états. Nous employons la lettre \(n\) par cohérence avec les suites mais comme le processus modélise une évolution dans le temps, nous aurions pu choisir \(t.\)
\(X_0\) suit une loi de probabilité \(\mathscr{L}(p_1, p_2,...,p_k).\)
La probabilité qu'un évènement survienne ne dépend que du présent. Les états précédents du processus n'ont aucun impact. On dit que c'est une suite sans mémoire.
Soit \(T\) une matrice de transition (matrice carrée stochastique).
Le théorème s'appuie sur les probabilités conditionnelles : \(P_{\{X_n = i\}}(X_{n+1} = j) = a_{ij}\) avec \(a_{ij}\) coefficients de \(T.\) On peut le démontrer par récurrence (la démonstration ne figure pas sur ce site).
D'accord, ce n'est pas très compréhensible pour tout le monde. Mais lorsque le processus est illustré il devient très clair.
Dans le cas le plus simple, il n’existe que deux états \(k.\) Voici l’exemple d’un extrait d’énoncé de l’épreuve du bac ES d’Amérique du sud, novembre 1998, enseignement de spécialité.
Exemple
- À partir de 1997, une association d’aide à la recherche médicale envoie chaque année à monsieur X un courrier pour l’inviter à l’aider financièrement par un don.
Monsieur X a répondu favorablement en 1997 en envoyant un don. On admet que, chaque année à partir de 1998, la probabilité pour que monsieur X fasse un don est égale à 0,9 s’il a fait un don l’année précédente et à 0,4 s’il n’a rien donné l’année précédente.

L’exercice complet est résolu en page de probabilités et suites (vous pourrez y lire la suite de l’énoncé) mais d’une autre manière que celle qui sera employée ici. D’ores et déjà, on voit bien qu’une variable prend à dates ou périodes régulières (des années) un nombre discret d’états possibles, en l’occurrence deux états (don ou pas don).
Un graphe probabiliste résume le processus.
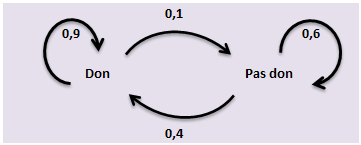
En bonne logique, la somme des poids des arêtes qui partent d’un même sommet vaut 1.
Comme nous l'avons vu, le processus peut aussi se résumer par une matrice de transition \(T\) avec en ligne les sommets de départ et en colonne les sommets d’arrivée, les coefficients de \(T\) étant les poids des arêtes.
\[T = \left( {\begin{array}{*{20}{c}}
{0,9}&{0,1}\\
{0,4}&{0,6}
\end{array}} \right)\]
Établissons pour chaque année la probabilité que M. X fasse un don.
Pour cela, il faut d’abord multiplier la matrice ligne de l'état initial avec la matrice de transition \(T\) avec l’état initial, puis multiplier le résultat obtenu par \(T\) autant de fois qu'on le désire. Si l’on remarque que les valeurs de la matrice convergent, bingo !
Notez que l’état initial de la matrice n’impacte pas l’état « final » (on dit que la chaîne est ergodique). Ceci est parfaitement logique, nous avons vu que le processus était sans mémoire.
Dans notre exemple, l’état initial correspondait à une année de générosité. On notera l’année 1997 avec un indice 1. Donc \({P_1} = \left( {\begin{array}{*{20}{c}}
1&0
\end{array}} \right).\)
Attention, un état initial ne reflète pas toujours une situation binaire comme ici (voir l’exemple de la page sur les graphes et matrices).
En 1998, on observe donc les probabilités suivantes : \({P_2}\) \(=\) \({P_1} \times T\) \(=\) \(\left( {\begin{array}{*{20}{c}}
{0,9}&{0,1}
\end{array}} \right)\)
Bon, pour cette année, il n'était pas nécessaire de multiplier des matrices. Juste de lire l'énoncé.
En 1999, elles évoluent encore :
\({P_3}\) \(=\) \({P_2} \times T\) \(=\) \(\left( {\begin{array}{*{20}{c}}
{0,9}&{0,1}
\end{array}} \right) \times \left( {\begin{array}{*{20}{c}}
{0,9}&{0,1}\\
{0,4}&{0,6}
\end{array}} \right)\) \(=\) \(\left( {\begin{array}{*{20}{c}}
{0,85}&{0,15}
\end{array}} \right)\)
Vous pouvez vérifier que l’on tend progressivement vers la matrice \(\left( {\begin{array}{*{20}{c}} {0,8}&{0,2} \end{array}} \right).\) D'ailleurs, on obtient directement ce résultat avec une puissance élevée de \(T.\)
Conclusion : après quelques années, la probabilité que ce généreux M. X fasse un don se stabilise autour de 0,8. Par ailleurs, M. X nous montre tout aussi généreusement ce qu'est un état stable.
Si vous avez compris le principe, vous pouvez passer à l'exercice sur les processus aléatoires, un peu moins facile.
En pratique, le champ des chaînes de Markov se limite rarement à un choix binaire et des matrices de transition \(10 \times 10\) ne sont pas rares dans les applications économiques…
Précisons toutefois que tous les processus ne se stabilisent pas.
Suite divergente
Ce qui suit n'est pas exigible au programme de terminale.
Soit une matrice de transition du type suivant :
\[T = \left( {\begin{array}{*{20}{c}}
A&0\\
0&B
\end{array}} \right)\]
\(A\) et \(B\) sont deux sous-matrices carrées ; \(T\) peut donc être repésentée par deux sous-graphes disjoints. On parle alors de matrice réductible. Soit l’état initial est dans \(A\) et il est impossible de trouver \(B,\) soit c’est l’inverse.
Les blocs d’une matrice de type périodique se présentent ainsi (ici, ce sont les sous-matrices nulles qui sont carrées) :
\[T = \left( {\begin{array}{*{20}{c}}
0&A\\
B&0
\end{array}} \right)\]
Soit on se trouve dans \(A,\) soit dans \(B.\) Mais on n’observe aucune convergence.
La preuve en exemple :
\[T = \left( {\begin{array}{*{20}{c}}
0&0&{0,1}&{0,8}&{0,1}\\
0&0&{0,3}&{0,7}&0\\
{0,4}&{0,6}&0&0&0\\
{0,1}&{0,9}&0&0&0\\
{0,6}&{0,4}&0&0&0
\end{array}} \right)\]
\[{T^3} = \left( {\begin{array}{*{20}{c}}
{0,1882}&{0,8118}&0&0&0\\
{0,1881}&{0,8119}&0&0&0\\
0&0&{0,2628}&{0,7186}&{0,0186}\\
0&0&{0,2622}&{0,7189}&{0,0189}\\
0&0&{0,2632}&{0,7184}&{0,0184}
\end{array}} \right)\]
Si sa matrice est irréductible et apériodique, la chaîne de Markov est ergodique.
Applications
Le champ d’application des chaînes de Markov est vaste. Pour s’en tenir à quelques utilisations en entreprise, mentionnons le marketing (probabilités de réachat), les ressources humaines (jeu des promotions et de l’effet de noria), le risque de crédit (évolution prévisionnelle des ratings), etc.
