Coordonnées cartésiennes et polaires
Il existe deux façons de localiser un point dans un plan (non, pas un plan de ville sur lequel on se situe grâce à la pastille « vous êtes ici » mais celui qui est muni d’un repère orthonormé). La première est d’utiliser ses coordonnées cartésiennes, c’est-à-dire son abscisse et son ordonnée. La seconde est d'utiliser ses coordonnées polaires, en se servant pour cela de la longueur d’un vecteur par rapport à l’origine et par l’angle orienté formé par ce vecteur et l’axe horizontal (pris à droite de l’origine). Dans la mesure où un repérage polaire ne requiert pas une abscisse et une ordonnée, on parle de repère polaire \((O\,;i).\) L’origine est appelé le pôle. Mais comment passer de l’une à l’autre de ces deux possibilités de localisation ?
Coordonnées polaires
Juste un mot sur la technique MANUELLE de placement d’un point sur un plan avec les coordonnées polaires : la construction du point \(M\left(3\,;\frac{\pi}{2}\right),\) par exemple, nécessite d’abord une transformation de l’angle \(\frac{\pi}{2}\) en degrés (donc 90°) puis, à l’aide d’un rapporteur, de placer un point correspondant à l’angle à partir de l’origine, de relier ces deux points et finalement de mesurer une longueur de trois unités sur cette droite à partir de l'origine. En l’occurrence, les coordonnées cartésiennes obtenues sont \((0\,;3).\)
Certes, les points ne sont pas toujours aussi simples à construire quoique la conversion entre cartésien et polaire n’a rien de compliqué. Celle-ci est enseignée en terminale mais nul besoin de passer par une filière scientifique pour comprendre le mécanisme. Cette page n’aborde pas les coordonnées polaires des nombres complexes, sujet réclamant un peu plus de bagage mathématique.

Du polaire au cartésien
Dans ce sens, la conversion est immédiate. Si les coordonnées polaires de \(M\) sont \((r\,;\theta),\) les coordonnées cartésiennes sont \(M(r\cos \theta\,; r \sin \theta).\)
\(r\) est le rayon polaire et, bien sûr, \(\theta\) est l’angle orienté.
Exemple : construire le point \(A(0,5\,;\frac{5\pi}{6}).\)
Attelons-nous à la tâche de deux façons, d’une part en obtenant des coordonnées cartésiennes et d’autre part en traçant un cercle.
Sachant que \(\cos\frac{5\pi}{6} = -\frac {\sqrt 3}{2}\) et que \(\sin\frac{5\pi}{6} = 0,5,\) on obtient \(A\left( { - \frac{{\sqrt 3 }}{4};0,25} \right).\)
Sur un cercle centré sur l’origine et dont le rayon est de 0,5, le point \(A\) se situe sur \(\frac{5\pi}{6}\) qui apparaît sur tout bon cercle trigonométrique en état de marche.
Du cartésien au polaire
Le calcul du rayon est assez évident. La formule est une simple application de l’incontournable théorème de Pythagore.
\(r = \sqrt{x^2 + y^2}\)
Quant à la mesure de l’angle…
\(\left\{ {\begin{array}{*{20}{c}} {\cos \theta = \frac{x}{r}}\\ {\sin \theta = \frac{y}{r}} \end{array}} \right.\)
La solution est immédiate si l’on a la bonne idée d’utiliser l’arc-tangente. Mais les formules différent selon les signes de \(x\) et \(y\) et en fonction de l’intervalle dans lequel on souhaite se situer. Habituellement, on ne tourne pas autour du cercle trigonométrique comme on tourne une béchamel : on se contente d’une mesure principale (entre \(–\pi\) et \(pi\) ou d’une mesure positive (entre \(0\) et \(2\pi)\). Si l’on cherche une mesure principale, les formules sont les suivantes :
Si \(x > 0,\) \(\theta = \arctan\frac{y}{x}.\) Si \(x < 0\) et \(y \geqslant 0,\) \(\theta = \arctan\frac{y}{x} + \pi.\) Si \(x < 0\) et \(y < 0,\) \(\theta = \arctan\frac{y}{x} - \pi.\) Ajoutons les cas particuliers où \(x = 0.\) Alors soit \(y\) est positif et \(\theta = \frac{\pi}{2},\) soit il est négatif et \(\theta = -\frac{\pi}{2}.\)
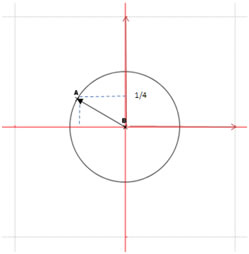
Exemple : soit le point \(A\) de coordonnées cartésiennes \(\left( { - \frac{{\sqrt 3 }}{4}\,;0,5} \right).\) On l’a tous reconnu, c’est le même que celui de l’exemple précédent. Retrouvons ses coordonnées polaires.
On en connaît le rayon...
\(r = \sqrt {{{\left( { - \frac{{\sqrt 3 }}{4}} \right)}^2} + {{\left( {\frac{1}{4}} \right)}^2}}\) \(= \sqrt {\frac{3}{{16}} + \frac{1}{{16}}}\) \(= \sqrt {\frac{1}{4}} = \frac{1}{2}\)
Et l’angle ? Son cosinus est égal à la moitié de \(-\frac{\sqrt{3}}{4},\) donc \(-\frac{\sqrt{3}}{2}.\) Son sinus vaut \(\frac{0,25}{0,5},\) donc 0,5. Quel angle correspond au cahier des charges ? Un coup d’œil sur le cercle trigonométrique nous indique \(\frac{5\pi}{6}.\)
Plus rapide, une simple calculatrice permet de calculer l’arc-tangente (tan-1) :
\({\tan ^{ - 1}}\left( {\frac{{\frac{1}{4}}}{{\frac{{ - \sqrt 3 }}{4}}} + \pi } \right)\) \(= \frac{{5\pi }}{6} \approx 2,618\)
Précision : on trouve aussi les termes de module (plutôt que rayon ou distance) et d’argument (plutôt qu’angle orienté). C'est ce vocabulaire qui est utilisé dans le cadre des nombres complexes.
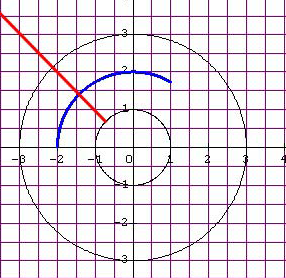
Exercice : représenter les points vérifiant les coordonnées polaires \(r > 1\) et \(\theta = \frac{3\pi}{4}\) (en rouge) ainsi que \(r = 2\) et \(\theta \in \left[ {\frac{\pi }{3};\pi } \right]\) (en bleu).
Corrigé :