Mesure et propriétés des angles orientés
Faisons un petit tour du côté d’un sujet qui occupe les élèves de première générale et de premières STI2D - STL pendant une semaine ou deux (« petit tour » étant juste une façon de s’exprimer, un tour mesurant \(2\pi.\) Ou alors le « petit » tour implique un rayon inférieur à 1. Enfin bref).
Cette page complète l'introduction à la trigonométrie.
Rappels
Lorsqu'un angle est mesuré en degrés, il n’a aucun sens. Non qu’il soit insensé mais peu importe s’il est mesuré de gauche à droite ou de droite à gauche (voir page trigonométrie en degrés).

Rappels : un angle dont la valeur est comprise entre l’angle nul (0°) et l’angle plat (180°) est saillant (aigu si inférieur à l’angle droit de 90°, obtus sinon). Entre 180° et 360°, il est rentrant. L'angle plein mesure 360°. Deux angles sont égaux si leurs côtés sont superposables.
Angle orienté
Pour déterminer l’angle que forment deux vecteurs \(\overrightarrow u \) et \(\overrightarrow v, \) on choisit un même point \(O\) duquel on les fait partir tous deux, \(O\) étant considéré comme le centre d’un cercle. Le rayon du cercle est la norme. Les deux droites qui sont les supports des vecteurs croisent le cercle normé en deux points \(A\) et \(B.\) Mais l’angle est cette fois ORIENTÉ selon qu’on le mesure entre \(\overrightarrow u \) et \(\overrightarrow v \) ou entre \(\overrightarrow v \) et \(\overrightarrow u \) (angle opposé). On le note \((\overrightarrow u ,\overrightarrow v ) = (\overrightarrow {OA} ,\overrightarrow {OB} ).\)
Pour faire le lien entre un angle et une longueur, on a créé le radian. Dans le système international, le radian est l’unité de mesure d’angle. Un tour complet (donc de 360°) est alors assimilé au périmètre d’un cercle dont le rayon est égal à la norme 1. Par conséquent, et c'est très important, \(360° = 2\pi\) radians. L’angle plat, qui est, rappelons-le au passage, la somme des trois angles d'un triangle, mesure \(\pi\) radians. Les principales correspondances sont les suivantes :

Les autres conversions sont faciles à obtenir puisqu’il suffit de procéder à une règle de trois à partir de celles-ci… Autre possibilité pour compléter ce tableau : le rapporteur trigonométrique.
On peut se promener sur le périmètre du cercle dans un sens ou dans l’autre. Le sens trigonométrique, positif, est celui du sens inverse des aiguilles d’une montre. Et là, on entrevoit la possibilité merveilleuse de fabriquer des angles NÉGATIFS (ce qui serait absurde avec une mesure en degrés).
Par ailleurs, si l’on ajoute ou si l’on ôte \(2\pi,\) on reste sur l’angle initial puisqu’un tour complet permet de revenir au point de départ. C’est pourquoi on ajoute \(2k\pi\) dès qu’une opération nous conduit à un angle puisque tous les multiples de cet angle par \(2k\pi\) sont égaux (on parle aussi d'angle modulo \(2\pi\). Précisons que \(k\) est un entier relatif ; ça ne fonctionne évidemment pas si \(k\) représente un nombre à virgule…
Du coup, il n’est pas nécessaire de manipuler des nombres élevés… Si par exemple un calcul nous conduit à un angle de \(3\pi,\) c’est la même chose que si l’on arrive à \(\pi.\) Généralement, on se satisfait de la mesure principale des angles, qui est comprise entre \(-\pi\) et \(\pi.\)
Propriétés
Les angles possèdent des propriétés qui semblent assez évidentes au commun des mortels qui veut bien se pencher sur la question, à commencer par la relation de Chasles : \((\overrightarrow u ,\overrightarrow w ) = (\overrightarrow u ,\overrightarrow v ) + (\overrightarrow v ,\overrightarrow w ).\)
En d’autres termes, si l’on additionne les angles formés par plusieurs parts de gâteaux, on obtient l’angle global des parts retenues.
Les autres propriétés sont elles aussi intuitives : \((\overrightarrow u ,\overrightarrow v )\) \(= - (\overrightarrow v ,\overrightarrow u )\) \(= ( - \overrightarrow u , - \overrightarrow v )\) et \(( - \overrightarrow u ,\overrightarrow v )\) \(= (\overrightarrow u , - \overrightarrow v )\) \(= (\overrightarrow u ,\overrightarrow v ) + \pi. \)
Si les deux vecteurs sont colinéaires et de même sens, l’angle formé par \(\overrightarrow u\) et \(\overrightarrow v\) est \(0 + 2 k\pi\) radians. Il est en revanche de \(\pi + 2k\pi\) si les vecteurs sont colinéaires mais de sens contraires.
Il est limpide que l’angle s’établit à \( \pm \frac{\pi }{2} + 2k\pi\) si les vecteurs sont orthogonaux.
Certaines transformations ne modifient pas les angles : translation et homothétie ne changent rien. En revanche, par réflexion, l’image d’un angle est son opposé.
Il est temps de passer à un exemple d'applications.
Exemple (relation de Chasles)
Cet exemple ne vise qu'à illustrer la relation de Chasles. Il s'appuie sur une figure géométrique et nous n'utiliserons pas les angles orientés (seulement les angles géométriques).
Soit un triangle équilatéral \(ABC.\) Le segment \([AB]\) est aussi l’hypoténuse d’un triangle rectangle isocèle \(ADB,\) tout comme \([AC]\) est l’hypoténuse d’un triangle rectangle \(ACE.\)
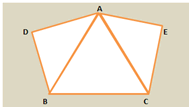
Quelle est la mesure de l'angle \(\widehat {CAB}\) ?
Les trois angles du triangle équilatéral sont égaux et comme la somme des angles de n’importe quel triangle est égale à \(\pi,\) l’angle \(\widehat {CAB}\) mesure \(\frac{\pi}{3}.\)
Quelle est la mesure de l’angle \(\widehat {EAD}\) ?
Les angles \(\widehat {BDA}\) et \(\widehat {AEC}\) sont droits et mesurent donc chacun \(\frac{\pi}{2}\) radians.
Comme les deux triangles \(ADB\) et \(ACE\) sont isocèles, leurs angles qui ne sont pas droits ont la même mesure, qui est \(\frac{\pi}{4}\) lorsqu’ils sont pris dans le sens trigonométrique (ainsi, la somme des trois angles est bien égale à \(\pi.\))
Par conséquent, \(\widehat {EAD}\) qui est égal à \(\widehat {EAC} + \widehat {CAB} + \widehat {BAD}\) en vertu de la relation de Chasles mesure \(\frac{\pi}{4} + \frac{\pi}{3} + \frac{\pi}{4}\) \(= \frac{5\pi}{6}.\)
Voir d'autres exemples et exercices en page de mesure principale.
La suite du programme de première fait découvrir le produit scalaire. Il est alors possible de calculer des angles dans un plan orthonormé (voir la page produit scalaire et mesures d'angles).
