Cercle trigonométrique : enroulement et rapporteur
Pour maîtriser les principes de la trigonométrie, il est primordial de comprendre comment fonctionne le cercle trigonométrique. C’est dans les classes de première générale et de première STI2D - STL que son mécanisme est enseigné.
Rappels
Rappel : la circonférence d’un cercle de rayon \(r\) est égale à \(2\pi r.\) Donc, si le rayon est égal à 1, cette circonférence mesure… \(2π.\) Oui, bravo !
Vous connaissez le principe de la géométrie analytique et vous êtes certainement habitué à étudier des figures dans un repère orthonormé \((O,I,J).\) Ainsi, un cercle de rayon 1 et de centre \(O\) ressemble à ceci (réalisation GeoGebra) :
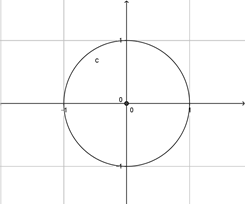
Principe
Sur ce repère, on peut tracer une droite \((d)\) d’équation \(x = 1.\) Si l’on enroule le cercle de façon à toujours garder un point de contact avec \((d),\) c’est comme si une mesure du cercle s’imprimait sur la droite. Cette « empreinte » apparaît d’ailleurs une infinité de fois puisque le cercle peut « rouler » à l’infini.

Nous avons rappelé que la circonférence du cercle valait \(2\pi.\) Donc, pour un point donné du cercle trigonométrique, cette même empreinte réapparaît chaque fois que l’on s’élève ou que l’on descend de \(2 \pi\) sur \((d).\)
Si le cercle s’enroule en s’élevant, ses points concordent avec des coordonnées positives de \((d)\) et s’il descend, ses points coïncident avec des valeurs négatives.
Imaginez que ci-dessous on enroule le cercle sur \((d),\) il doit vous paraître évident que le point \(M\) du cercle coïncide avec le point \(N\) de coordonnées \((1\,;\pi)\) puisque la moitié de la circonférence vaut \(\pi\). Selon le sens dans lequel le cercle s’enroule sur \((d),\) \(M\) se trouve aussi sur les points de coordonnées \((1\,;-\pi),\) \((1\,;3\pi),\) etc.
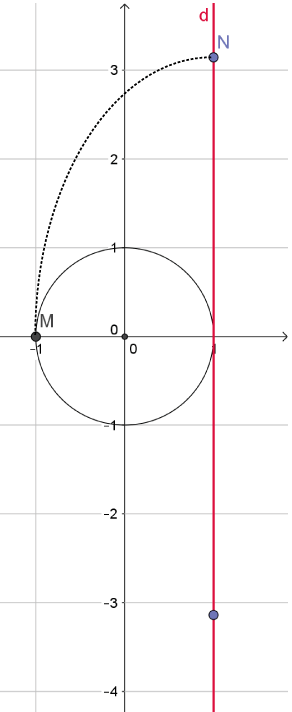
Ainsi, à chaque point de (\(d)\) est associé un point unique du cercle. Mais à chaque point \(M\) du cercle est aussi associé un angle \(\widehat O\) dont les côtés sont \(OI\) (avec \(I(1\,;0)\)) et \(OM.\)
Donc à chaque valeur lue sur (\(d)\) correspond une valeur d’angle. Nous avons vu que l’on enroulait le cercle sur la droite dans un sens ou dans l’autre. Attention, il existe un sens de rotation positif du cercle : le sens inverse des aiguilles d’une montre. Ci-dessous on forme un angle de 90° aussi bien en mesurant \(\widehat {OIC}\) que \(\widehat {OID}\) ; mais le point \(D',\) qui correspond sur (\(d)\) au point \(D\) du cercle a une valeur négative, en l’occurrence \(\frac{-\pi}{2}.\) Il correspond donc à -90°.
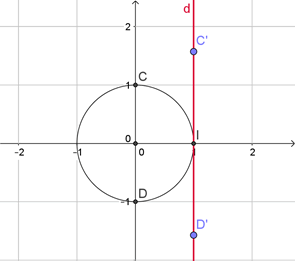
Il ne vous reste plus qu'à vous entraîner en page exercices de trigonométrie !
Le rapporteur trigonométrique
Le rapporteur trigonométrique est un instrument de mesure des angles en degrés et en radians. Si vous souhaitez vous en construire un facilement, téléchargez le logiciel gratuit Sine qua non 2.9.2 (lien ci-dessous), ouvrez le logiciel et cliquez sur le bouton qui ressemble à un rapporteur circulaire. Procédez aux réglages si vous le souhaitez. Il ne vous reste qu’à l’imprimer sur une feuille transparente.
http://patrice-rabiller.fr/SineQuaNon/menusqn.htm

