Fonctions à une variable et symétrie
Note préalable : si vous êtes en seconde, ce sujet vous sera beaucoup plus accessible en page d'introduction à la parité et si vous êtes en première générale, des exercices sur la parité des fonctions trigonométriques vous attendent les bras ouverts. Cette page est plus adaptée aux étudiants.
En statistiques, la symétrie d’une distribution autour d’une moyenne s’évalue par le coefficient d’asymétrie. En analyse, il ne s’agit pas d’estimer si une fonction est plus ou moins symétrique : elle l’est ou ou elle ne l'est pas. To be or not to be. Et de plus, les symétries sont de deux types (comme vous l'avez appris au collège en cours de géométrie).
Définition
On dit qu’une fonction \(f\) est paire si, quel que soit \(x\) appartenant à l'ensemble de définition, \(f(x) = f(-x)\) et qu’elle est impaire si \(f(-x) = -f(x).\)
Pourquoi nommer ces fonctions ainsi ? Tout simplement parce qu’une fonction puissance, donc de type \(f(x) = x^n\) (\(n\) entier naturel) est paire si \(n\) est pair et impaire si \(n\) est impair. Cette propriété s'étend aux puissances négatives.
Tracé
Dans l’étude d’une fonction, la recherche d’une éventuelle symétrie est conduite en amont, une fois l’ensemble de définition précisé. Si l’on peut prouver une symétrie, il suffit d’analyser une moitié seulement de la fonction. Les situations les plus simples nous renvoient au programme de seconde.
Pour tracer la courbe représentative d’une fonction paire, on utilise l’axe des ordonnées comme un miroir (symétrie axiale). Les fonctions ayant pour expressions \(f(x) = |x|,\) \(f(x) = x^2\) ou \(f(x) = \cos x \) sont des exemples simples de fonctions paires.
En revanche, c’est l’origine du repère (donc un point) qui sert de miroir pour tracer la courbe d’une fonction impaire (symétrie centrale). La fonction inverse, la fonction sinus ou encore la fonction cosécante en constituent des illustrations du plus bel effet.
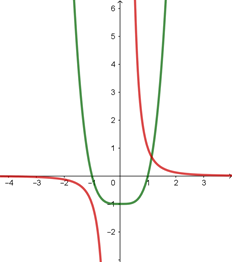
Voici la représentation graphique d’une fonction paire (en vert, \(f:x \mapsto x^4 - 1\) et d’une fonction impaire (en rouge, \(g: x \mapsto x^{-3}\)).
Propriétés
La somme et le produit de deux fonctions paires est une fonction paire. La somme de deux fonctions impaires est une fonction impaire. Mais le produit de deux fonctions impaires est une fonction paire.
D'une façon plus générale, toute combinaison linéaire de fonctions paires est une fonction paire, la même remarque s'appliquant aux fonctions impaires.
Aussi étonnant que cela puisse paraître, toute fonction définie sur \(\mathbb{R}\) peut être présentée comme la somme d'une fonction paire et d'une fonction impaire. Par exemple, les parties paire et impaire de la fonction exponentielle sont les fonctions sinus et cosinus hyperboliques.
La dérivée d'une fonction paire est impaire et inversement puisque si \(f(x) = f(-x),\) alors \(f'(x) = -f'(-x).\)
Soit \(a\) un réel. Si \(f\) est paire, alors \(\int_{ - a}^a {f(x)dx}\) \(=\) \(2\int_0^2 {f(x)dx} \)
Et si elle est impaire \(\int_{ - a}^a {f(x)dx} = 0\)
Axes de symétrie
L'axe de symétrie d'une courbe représentative d'une fonction n'est pas toujours l'axe des ordonnées. Si cet axe a pour équation \(x = a\) avec \(a \in \mathbb{R},\) c’est que \(f(a + x) = f(a - x),\) ou, ce qui revient au même, \(f(2a - x) = f(x).\) Pour prouver la symétrie, soit on démontre cette égalité, soit on opère un changement de variable avant d’établir que la nouvelle fonction est paire.
Soit \(a,\) \(b\) et \(c\) réels. La parabole représentative d'une fonction du second degré \(f:x \mapsto ax^2 + bx + c\) admet un axe de symétrie d’équation \(x = -\frac{b}{2a}.\)

Centres de symétrie
De même un point différent de l’origine peut être centre de symétrie. Si une fonction \(f\) vérifie l'équation \(f(2x_0 - x) = 2y_0 - f(x),\) c’est que le point de coordonnées \((x_0\,;y_0)\) est centre de symétrie de la courbe. Là encore, on peut le prouver soit en utilisant la formule, soit en démontrant que la fonction devient impaire après avoir opéré un judicieux changement de variable.
L'hyperbole représentative de la fonction homographique \(f: x \mapsto \frac{ax + b}{cx + d}\) admet un centre de symétrie au point de coordonnées \((-\frac{d}{c}\,; \frac{a}{c}).\)
Pour terminer, mentionnons pour mémoire les axes de symétrie entre courbes de deux fonctions différentes. Lorsque cet axe est la première bissectrice, les fonctions sont dites réciproques (logarithme népérien et exponentielle, par exemple). L'axe des abscisses est quant à lui un axe de symétrie entre \(f(x)\) et son opposée \(-f(x).\)
Exemple
Mais on ne va pas se quitter comme ça. Examinons un petit exercice facile. Soit la fonction suivante :
\(f:x \mapsto \frac{1}{\sigma \sqrt{2 \pi}} \exp \left[-\frac{1}{2}\left(\frac{x - m}{\sigma}\right)^2 \right]\)
Les plus perspicaces auront reconnu la fonction de densité de cette bonne vieille loi normale. Vérifions qu’elle est paire pour \(x = m.\)
\(f(2m - x)\) \(=\) \(\frac{1}{\sigma \sqrt{2 \pi}} \exp \left[-\frac{1}{2}\left(\frac{2m - x - m}{\sigma}\right)^2 \right]\)
\(\Leftrightarrow f(2m - x)\) \(=\) \(\frac{1}{\sigma \sqrt{2 \pi}} \exp \left[-\frac{1}{2}\left(\frac{x - m}{\sigma}\right)^2 \right]\)
Or, \(\left( \frac{m - x}{\sigma}\right)^2 = \left(\frac{x - m}{\sigma}\right)^2\)
Donc \(f(2m - x) = f(x)\) et la courbe représentative évolue symétriquement à l'axe d'équation \(x = m.\) Évidemment, si la loi est centrée, sa fonction de densité est paire.
Voir aussi l'exercice 1 de la page d'exercices avec la fonction sinus.
