Boucles "pour" et "tant que"
Si vous vous initiez à l’algorithmique, vous ne pouvez pas passer à côté des instructions conditionnelles et des boucles.
Le principe des boucles, ou calcul itératif, consiste à répéter les mêmes instructions un certain nombre de fois.
Il en existe deux types : la boucle bornée POUR (le nombre de traitements est expressément défini par l’utilisateur) et la boucle non bornée TANT QUE (on ignore a priori combien de fois le bloc d’instructions sera répété). En anglais et dans plusieurs langages de programmation, ces boucles sont respectivement nommées for et while. On appelle itération un processus chaque fois qu’il se répète.
Dans les deux cas, l’algorithme comporte une variable compteur habituellement notée i ou I.

La boucle bornée
Amusons-nous à calculer la somme des n premiers entiers naturels (nombres triangulaires).
n est une valeur choisie par l’utilisateur de l’algorithme.
En langage naturel, l’algorithme peut ressembler à ceci :
| saisir n P ← 0 pour i variant de 1 à n P ← P + i fin pour afficher P |
Explications. Nous avons besoin de deux variables, plus le compteur : soit le nombre de boucles n et le montant de la somme des premiers entiers après chaque itération P. L’algorithme part de zéro. À chaque itération, une nouvelle valeur de P écrase la précédente en ajoutant 1 (puisque i est incrémenté de 1 à chaque fois).
Par exemple si n \( = 2\) il y a deux itérations. Lors de la première, donc avec i \(= 1\), \(P\) prend la valeur \(0 + 1 = 1\) et lors de la seconde où i \( = 2\), \(P\) prend la valeur \(1 + 2 = 3.\) Le traitement de l’algorithme s’arrête ici puisque la valeur de i devient égale à celle de n. L’écran affiche alors 3, soit la somme des deux premiers entiers 1 et 2.
Comment programmer une calculatrice TI (en l’occurrence une TI-83 Premium CE) pour faire fonctionner cet algorithme ?
Pour les instructions non liées aux boucles, revoir l’initiation à la programmation sur TI au cas où vous auriez quelques trous de mémoire.
La création du programme débute par la demande de saisie de N et se poursuit par l’affectation de la valeur 0 à la variable P (touche sto). L’instruction POUR est donnée par For (touche prgm, sous-menu CTL, choix 4). Pensez à indiquer la fin de la boucle (instruction End).
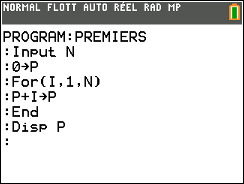
Ci-dessous, le programme affiche la somme des 50 premiers entiers :
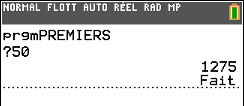
La programmation des boucles avec calculatrice Casio est traitée en page de boucles avec Casio.
Voir aussi les boucles for avec Python.
La boucle non bornée
L’utilisateur ne connaît que la condition de sortie. Il ignore a priori le nombre d’itérations nécessaire pour y parvenir.
À la fin de la boucle, la condition est vérifiée. Si elle est remplie le processus s’arrête ; si elle ne l’est pas une nouvelle itération est exécutée.
Ci-dessous se trouve un exercice traité en page de suites géométriques avec Excel. Mathématiquement, il est du niveau d’une classe de première mais il est possible de le résoudre dès la seconde en programmant une calculatrice.
Énoncé : en cette année 1800, Cornélius aimerait bien s’acheter le magnifique bœuf qu’il a repéré à la foire aux bestiaux. Hélas, celui-ci coûte 600 francs et il ne dispose que de 420 F. Il place cette somme à un taux d’intérêt de \(4\%\) (intérêts composés) afin de pouvoir se payer un jour l’objet de sa convoitise.
Déterminer en quelle année Cornélius a pu acheter ce fameux bœuf.

Éléments de correction : un intérêt composé de \(4\%\) signifie qu’il faut multiplier chaque année le montant budgété par 1,04. Avec ce taux d’intérêt, il s’agit de déterminer une valeur de n (nombre d’années) pour qu’une somme de 420 F se transforme en 600 F.
| n ← 1800 S ← 420 tant que S < 600 S ← S × 1,04 n ← n + 1 fin tant que afficher n |
Explications : le somme dont dispose Cornélius est donnée par la variable S. Dans cet exercice, rien n’est demandé à l’utilisateur : l’année de départ est 1800, le taux d’intérêt de \(4\%\) et la somme de départ de 420 F. Donc pas d’entrée mais seulement des initialisations. Tant que la somme n’a pas atteint 600, on lui applique le taux d’intérêt annuel. C’est-à-dire que la valeur de la variable S est multipliée par 1,04 (ce taux ne change jamais, 1,04 est donc écrit « en dur » dans le programme). La précédente valeur de S n’est pas conservée ou affichée par l’algorithme. Si le taux est appliqué, alors l’année est incrémentée de 1 (on passe à l’année suivante). Là encore, la nouvelle valeur remplace la précédente. Si S atteint ou dépasse 600, le processus passe à la ligne « fin tant que » et affiche l’année.
Comme vous savez à présent manipuler comme un maître votre calculatrice, nous ne détaillerons pas le mode d’emploi (rappelons juste que le symbole < s’obtient avec la touche test). Voici une suggestion d’écriture du programme :
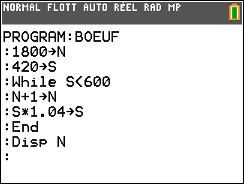
Faites-le tourner. L’écran affiche 1810. C’est donc en l’an 1810 que Cornélius aura les moyens de s’acheter le bœuf.
Voir aussi la fonction logarithme avec algorithme (sujet de bac S).
