Loi de Weibull à deux paramètres
Waloddi Weibull était un mathématicien suédois d’origine allemande (mort à Annecy en 1979). Vous vous en fichez peut-être, mais s’il vous prenait l’idée de lire cette page à voix haute, ça vous évitera de prononcer son nom à l’anglaise.
La loi de Weibull
Bref, Weibull a donné son patronyme à une loi de probabilité continue appliquée aux durées de vie. C’est donc dans le contrôle de fiabilité que les entreprises ont tendance à l’utiliser, et plus précisément lorsque le taux de défaillance évolue comme une puissance du temps (ce qui est le cas le plus courant). Rappelons que lorsque ce taux est constant, on utilise la loi exponentielle, forme particulière de celle de Weibull, et lorsque le taux augmente proportionnellement au temps, c’est la distribution de Rayleigh qui est employée.
Les paramètres
La loi de Weibull repose sur deux paramètres positifs, l’un de forme et l’autre d’échelle de temps. Leurs dénominations diffèrent selon les ouvrages et les logiciels. La loi de Weibull à trois paramètres prend en compte la "localisation", c'est-à-dire un éventuel décalage du départ de la courbe par rapport à l'origine (soit à gauche soit à droite).
Adoptons alpha pour le paramètre de forme, lambda (ou plutôt son inverse) étant celui de temps. La fonction de répartition est la suivante : \(F(x) = 1 - \exp(-(\lambda x)^{\alpha})\)
Et bien sûr, \(F(x) = 0,\) \(\forall x < 0.\) La détermination de sa fonction de densité est un exercice de dérivation avec exponentielles.
Le paramètre \(α\) est habituellement supérieur à 1 : le taux de défaillance croît avec le temps. S’il est inférieur, c’est pendant le rodage que les risques de défaillance sont élevés et s’il est égal à 1, on retombe sur la loi exponentielle.
On trouve plus souvent la formule écrite avec \(\frac{1}{λ}.\) Question de convention. J’ai préféré celle-ci par cohérence avec la loi exponentielle. Ce paramètre est exprimé dans la même unité de temps que \(x.\)
Sa médiane : \(\displaystyle{\frac{(\ln 2)^{\frac{1}{\alpha}}}{\lambda}}\)
Mais tout ceci reste très théorique. Les deux paramètres sont trop pudiques pour se dévoiler et les logiciels vont employer de savants et rusés algorithmes pour deviner qui ils sont. Personne ne le saura avec certitude...
Exemple
Illustrons ceci par l’édifiante et néanmoins fictive enquête sur la durée de vie de tondeuses pour chiens. Une enquête auprès de dix professionnels a montré que le nombre de chiens tondus variait sensiblement avant qu’une tondeuse ne rende l’âme dans la mesure où tous nos fidèles compagnons n’ont ni la même taille ni la même épaisseur de poil.
| Chiens tondus |
| 1 020 |
| 1 342 |
| 1 601 |
| 1 687 |
| 1 871 |
| 1 918 |
| 1 964 |
| 2 009 |
| 2 080 |
| 2 211 |
Nous supposons ici que tous les appareils sont « morts » mais certains logiciels permettent d’inclure des appareils qui fonctionnent encore au moment du relevé. Nous avons ainsi ABRÉGÉ la durée d’observation de certaines données (« censored » en anglais, attention à ne pas faire de contresens sur ce mot !).

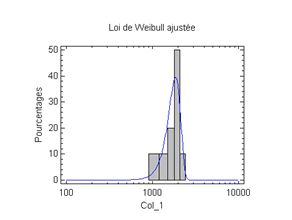
Commençons par explorer les sorties de Statgraphics Centurion. Par défaut, la méthode d’analyse est celle du maximum de vraisemblance. Le logiciel permet toutefois d’utiliser d’autres techniques (régression sur les rangs et Webayes).

C’est avec le test de Kolmogorov-Smirnov que Statgraphics vérifie par défaut la probabilité d’adéquation de la distribution observée à la distribution d’une loi de Weibull dont les paramètres sont indiqués ci-dessus (le logiciel permet aussi d’autres tests d’adéquation).

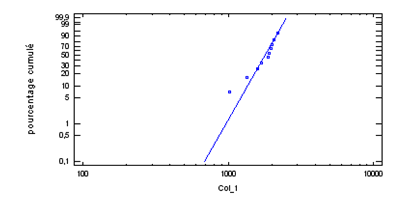
Le graphique de Weibull, permet une visualisation facile, sur un papier particulier, de l’adéquation entre la distribution et la fonction de répartition ramenée à une droite (à l’instar de la droite de Henry, bien pratique pour estimer l’adéquation à une loi normale).
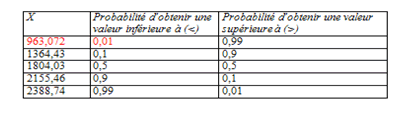
Et pour ne pas perdre de vue l’aspect opérationnel de nos analyses, voyons un tableau qui intéressera le responsable de la qualité :
Notez que d'autres graphiques peuvent être édités par Statgraphics : fonctions de survie, de risque, etc.
Pour conclure, vous avez là quelques premiers éléments sur une loi de durée de vie. Voir en complément la page sur les méthodes d'analyse d'une loi de Weibull où, sur le même exemple, la régression sur les rangs et le logiciel WEIBULL++ sont utilisés.
