Exercices de probabilités conditionnelles
Deux exercices sur les probabilités conditionnelles spécialement rédigés à l’attention des élèves de premières technologiques. L’un est prétexte à réaliser un tableau croisé avec tableur, l’autre est une application des tests diagnostiques.
Énoncé 1 : probabilités avec Excel
Pour vous entraîner aux tableaux croisés, reproduisez le fichier ci-dessous sur une feuille Excel ou OpenOffice (allez, ce n’est pas très long !). Il s’agit des lettres de l’alphabet telles qu’on les trouve dans un jeu de scrabble francophone avec le nombre de jetons correspondants, leur type (voyelle, consonne ou joker respectivement notés \(V,\) \(C\) et \(J\)) et leur valeur : \(E\) pour « élevée » (8 ou 10 points) et \(F\) pour « faible » (0 à 4 points). Pour tout l’exercice, les résultats seront arrondis au centième.
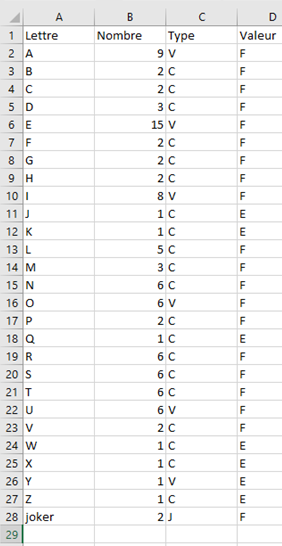
- Réaliser un tableau croisé avec un tableur. On indiquera le nombre de jetons selon le type (en ligne) et selon la valeur (en colonne).
- On tire une lettre au hasard. Quelle est la probabilité que ce soit une consonne ?
- Calculer \(P(V \cup E)\) et interpréter le résultat.
- Sachant que le jeton tiré est une consonne, quelle est la probabilité qu’elle soit de valeur élevée ?
Corrigé 1
1 - Il faut sélectionner les trois dernières colonnes du tableau puisque nous n’avons pas besoin de la première pour la question qui nous est posée.
Le mode d’emploi figure en page de tableaux croisés dynamiques mais, au cas où vous ne l’auriez pas lu, voici comment poursuivre le travail : Insertion puis tableau croisé dynamique. Si la plage est déjà sélectionnée, entrée.
Cochez les trois champs qui nous intéressent puis cliquez-glissez-les dans les bonnes zones comme ci-dessous.
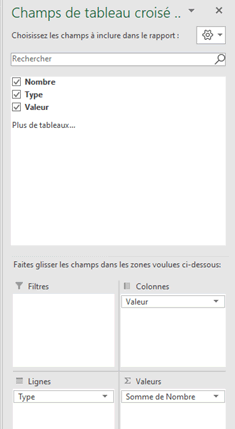
Le tableau obtenu n’est pas très joli :

Vous pouvez changer les intitulés dans le tableau et modifier la largeur des cellules (en cliquant dans la barre grise de noms de colonnes puis en se positionnant entre deux colonnes pour que le curseur prenne une forme de croix). Le tableau obtenu n’est pas extraordinairement beau mais on s’en contentera.
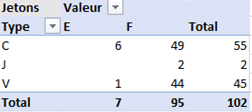
2 - \(P(C) = \frac{55}{102} ≈ 0,54.\) La probabilité que le jeton tiré soit une consonne est de 0,54 (arrondi au centième).
3 - \(P(V ∪ E)\) \(= P(V) + P(E) - P(V ∩ E)\) \(=\frac{45}{102} + \frac{7}{102} - \frac{1}{102}\) \(= 0,5.\)
La moitié des jetons sont soit des voyelles soit des lettres de valeur élevée (soit les deux à la fois).
4 - \(P_C(E)\) \(= \frac{C ∩ E}{C}\) \(= \frac{6}{55}\) \(≈ 0,11.\)
Sachant que le jeton tiré est une consonne, la probabilité qu’il soit de valeur élevée est de 0,11 (arrondi au centième).
Énoncé 2 : test diagnostique
Un laboratoire met au point un test permettant de détecter une maladie dont \(0,1\%\) de la population est atteinte. Les statistiques montrent que le taux de faux positif (résultat positif alors que la personne n’est pas malade) est de \(5\%.\) Que pensez-vous de ce test ? On supposera qu’il n’y a pas de faux négatif et on pourra raisonner à partir d’une population de 1000 personnes.
Corrigé 2
On pourrait penser que le test est bon, que le risque d’erreur est faible... Erreur ! Ce test ne vaut rien ! Pourquoi ?
Sur 1 000 personnes, le test sera positif pour 1 personne (soit \(1000 \times 0,1\%\)) à raison et sur 50 personnes à tort. Il sera donc positif dans 51 cas.
La probabilité que le patient soit malade sachant que le test est positif s’établit donc à \(\frac{1}{51} ≈ 0,02\) (moins de \(2\%\)).
