Construction des tables de Poisson
Aujourd’hui, on se sert d'un ordinateur ou d'une calculatrice pour connaître les valeurs prises par une loi de probabilité usuelle. Toutefois, il peut être pratique de disposer des bonnes vieilles tables. Nous verrons ici comment construire celles de la loi de Poisson. Cette page n’est donc pas une référence avec tables complètes (si tant est qu’elles existent) mais elle explique comment les construire avec un tableur. Et après le mode d’emploi de la construction, celui de l’utilisation avec de petits exemples. Vous voilà parfaitement outillé.
Notez que les manuels de statistiques présentent souvent des tables de loi de Poisson en annexe, soit pour \(P(X = k)\) soit pour \(P(X \leqslant k).\) Si vous les construisez vous-même, vous aurez les deux.
Probabilités de Poisson : \(P(X = k)\)
Les tables font intervenir le paramètre \(λ\) (lambda) ainsi que la valeur prise par la variable aléatoire. Vous pouvez construire des tables plus ou moins fines en déterminant pour \(λ\) un pas de 1, de 0,1 ou autre.
Ci-dessous c’est un extrait de 4 à 6 avec un pas de 0,2 qui illustre sa construction avec Excel.
Après avoir rempli la ligne des valeurs de \(λ\) et la colonne des valeurs de \(k,\) positionnez-vous sur la première cellule de la table (ici B3) et renseignez la fenêtre qui s'affiche lorsque vous sélectionnez la loi de Poisson dans les fonctions statistiques. Soit la valeur \(k\) de la variable aléatoire \(X,\) puis l’espérance \(λ,\) puis 0 puisque pour l'instant nous construisons une table de probabilités non cumulées.
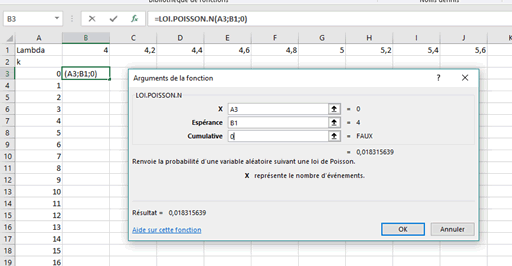
Avant de copier-glisser la formule dans l’ensemble de la table, insérez le symbole $ comme ceci :
=LOI.POISSON.N($A3;B$1;0).
Résultat :
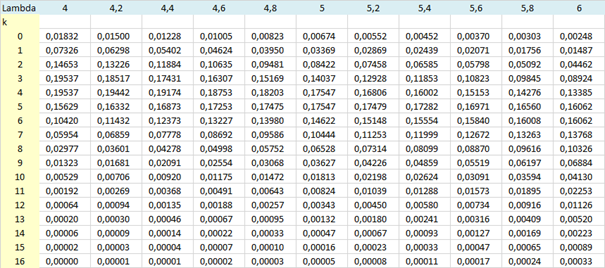
Par exemple, on sait qu’en moyenne cinq usagers se présentent à un guichet en l'espace de 10 mn et que ces arrivées suivent une loi de Poisson. La variable aléatoire est le nombre d’usagers arrivés pendant une période de 10 mn. Si vous regardez bien la colonne 5 (puisque la moyenne est égale à 5), vous constatez que les probabilités les plus élevées correspondent à quatre ou cinq arrivées. Si l’on souhaite connaître la probabilité que dix clients se présentent pendant ce laps de temps de 10 mn, on la trouve à l’intersection de la colonne 5 et de la ligne 10. Soit \(P(X = 10)\) \(=\) \(0,01813.\)
Probabilités cumulées : \(P(X \leqslant k)\)
Pour construire la table, rien de simple. Il suffit de remplacer le 0 en fin de formule par 1 ce qui, pour Excel, signifie « cumulative ».
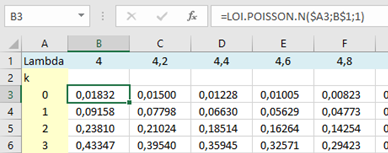
Exemple d’extrait de table :
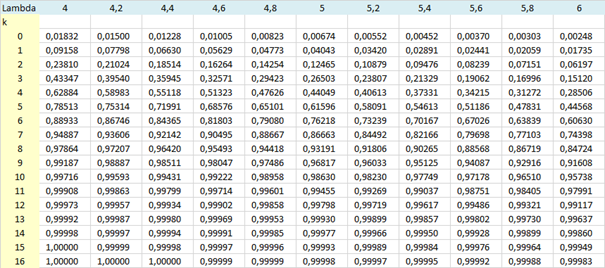
Dans une librairie, le nombre de manuels de maths et de statistiques vendus en une journée suit une loi de Poisson de paramètre 5. Quelle est la probabilité d’en vendre entre zéro et trois ?
La réponse figure en colonne 5 (puisque, dans cet exemple aussi, la moyenne est 5) et en ligne 3. Soit \(P(X \leqslant 3)\) \(=\) \(0,26503.\)
Quelle est la probabilité que le nombre de ventes soit compris entre 4 et 6 inclus ?
\(P(4 \leqslant X \leqslant 6)\) \(=\) \(P(X \leqslant 6) - P(X \leqslant 3)\) \(=\) \(0,76218 - 0,26503\) \(=\) \(0,49716.\)
Et pour terminer, une probabilité conditionnelle : quelle est la probabilité que le nombre de ventes soit au plus égal à sept sachant qu’elle est au moins égale à deux.
La probabilité que \(X\) soit au moins égale à 2 est la probabilité contraire d'être inférieure ou égale à 1.
On lit dans la table \(P(X \leqslant 1) = 0,04043.\) Donc \(P(X \geqslant 2)\) \(=\) \(1 - 0,0403\) \(=\) \(0,95957\) (l’avantage d’avoir vos tables sur Excel est aussi de réaliser ce type de calcul sur la même feuille sans avoir à recopier les probabilités).
\(P(1 \leqslant X \leqslant 7)\) \(=\) \(0,86663 - 0,04043,\) soit 0,82620.
Ainsi, \(P(X \leqslant 7 | X\geqslant 2)\) \(=\) \(\frac{0,8262}{0,95957}\) \(\approx\) \(0,861\)
Un autre extrait de table figure en page de loi de Poisson.
