Triangle de Pascal avec Python
Nous ne reviendrons pas sur les multiples propriétés de ce merveilleux outil qu’est le triangle de Pascal (d’ailleurs découvert bien avant Pascal). Celui-ci possède cependant une qualité qui n’a rien de mathématique : c’est un très bon support pour apprendre la programmation. En l’occurrence, il permet de s’exercer sur les listes et les boucles imbriquées.
Après un bref rappel sur la construction du triangle, nous étudierons un exemple d’algorithme en langage Python.
Rappel
Le triangle de Pascal se construit ainsi :
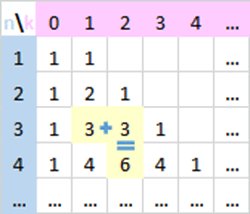
En termes de coefficients binomiaux :
\(\left( {\begin{array}{*{20}{c}}
{n - 1}\\
{k - 1}
\end{array}} \right) + \left( {\begin{array}{*{20}{c}}
{n - 1}\\
k
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
n\\
k
\end{array}} \right)\)
Construction avec python
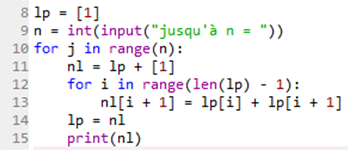
Avec Pyhon, on considère chaque ligne comme une liste dont les éléments sont définis par une autre liste, expression de la ligne précédente du triangle. La première ligne se résume à un seul 1. Donc nous initierons notre liste avec cette unique valeur (ligne 8 de la capture d’écran ci-après).
Le passage d’une ligne à la suivante est la partie la moins facile à programmer. D’abord, on remarque que chaque ligne du triangle possède un élément de plus que la précédente et que cet élément est 1. Donc on ajoute 1 pour passer d’une liste à la suivante (ligne 11 ci-dessous, avec 1 entre crochet puisque, bien qu’élément unique, c’est aussi une liste).
Hormis ce 1 final, chaque ligne, donc chaque liste, comporte \(n\) éléments.
L’algorithme sera construit sur deux boucles imbriquées que nous indicerons i et j. Soit lp la ligne précédente et nl la nouvelle ligne.
j correspond au nombre de lignes du triangle, en plus de la ligne 0 qui ne comporte qu’un seul 1, comme nous l’avons vu.
i dépend du nombre d’éléments d’une ligne. C’est l’indice de la boucle qui calcule \(lp - 1\) éléments d’une ligne. En termes de liste, nous pouvons réécrire la formule du coefficient binomial ainsi : lp[i] + lp[i+1] = nl[i+1]. La longueur est \(lp - 1\) car le dernier élément de la ligne \(lp\) ne peut pas s’additionner avec un élément à sa droite qui n’existe pas. On le voit sur l’illustration du rappel (en début de page) : lorsque \(n = 4\) seules trois valeurs sont calculées.
Ligne 15, le fait d’intégrer print à la boucle permet d’obtenir le triangle jusqu’à la valeur \(n\) entrée par l’utilisateur (ligne 9). Si cette instruction n’est pas indentée, seule la dernière ligne du triangle apparaît.
Exemple de sortie :
Coefficient binomial
Il est très facile d’extraire un coefficient binomial à partir du programme précédent. C’est le kème élément de la dernière liste calculée.
lp = [1]
n = int(input("pour n = "))
k = int(input("pour k = "))
for j in range(n):
nl = lp + [1]
for i in range(len(lp) - 1):
nl[i + 1] = lp[i] + lp[i + 1]
lp = nl
print(nl[k])
Libre à vous de reprendre ce programme et d’insérer une condition pour retourner un message d’erreur au cas où \(k\) serait supérieur à \(n.\)
Exemple de sortie :
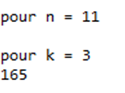
Nous le vérifions d’ailleurs sur la dernière ligne du triangle reproduit au-dessus (n’oubliez pas que la première colonne correspond à \(k = 0\)).
Variante du programme avec définition d'une fonction, dont vous trouverez une version complétée en page de loi binomiale avec Python.
n = int(input("pour n = "))
k = int(input("pour k = "))
def coeff(n,k):
lp = [1]
for j in range(n):
nl = lp + [1]
for i in range(len(lp) - 1):
nl[i + 1] = lp[i] + lp[i + 1]
lp = nl
return nl[k]
print(coeff(n,k))
Notez que vous pouvez aussi déterminer un coefficient binomial avec la formule qui comporte des factorielles. Voir le programme de combinaison de la page d’exercices de combinatoire.
