Propriétés du coefficient binomial
Lorsqu’on souhaite déterminer un nombre de combinaisons possibles, on calcule le coefficient binomial. Cette page ne présente pas un exposé complet sur ce petit bijou mathématique et n’a d’autre ambition que d’apporter une ressource aux élèves du secondaire.
Bien comprendre ce qu’est le coefficient binomial
Supposons une suite de \(n\) expériences aléatoires suivant un schéma de Bernoulli (succès ou échec). Nous ne nous préoccuperons pas des probabilités.
Ce schéma peut être visualisé grâce un arbre de dénombrement à \(n\) niveaux, chaque sommet générant deux branches.
Si l’on cherche le nombre de possibilités d’obtenir \(k\) succès (\(k\) étant bien sûr compris entre 0 et \(n\)), cela revient à compter le nombre de chemins qui satisfont à cette condition. Ce nombre nous est donné par le coefficient binomial.
Il s’écrit généralement \({\left( {\begin{array}{*{20}{c}} n\\ k \end{array}} \right)}\)
On lit « \(k\) parmi \(n\) ».
Propriétés
Propriété 1 : \({\left( {\begin{array}{*{20}{c}}
n\\
0
\end{array}} \right)}\) \(=\) \({\left( {\begin{array}{*{20}{c}}
n\\
n
\end{array}} \right)}\) \(=\) \(1\)
Traduction : il n’existe qu’un seul chemin pour n’obtenir que des succès et un seul pour n’obtenir que des échecs. C’est d’ailleurs suffisamment intuitif pour que nous ne nous étendions pas là-dessus.
Autre propriété : \({\left( {\begin{array}{*{20}{c}}
n\\
1
\end{array}} \right)} = n\)
Prenons l’exemple où \(n = 3.\) Quel est le nombre de possibilités d’avoir un seul succès ? On peut avoir un succès suivi de deux échecs, un échec suivi d’un succès puis d’un échec et enfin deux échecs suivis d’un succès. Parfait, on trouve bien trois possibilités.
Enfin, \({\left( {\begin{array}{*{20}{c}}
n\\
n-k
\end{array}} \right)} = {\left( {\begin{array}{*{20}{c}}
n\\
k
\end{array}} \right)}\)
S’il y a \(n - k\) succès, c’est qu’il y a \(k\) échecs. Là encore, c’est évident.
En revanche, la propriété suivante ne saute pas aux yeux. Elle est démontrée en page de relation de Pascal.
\({\left( {\begin{array}{*{20}{c}}
n+1\\
k+1
\end{array}} \right)} = {\left( {\begin{array}{*{20}{c}}
n\\
k
\end{array}} \right)} + {\left( {\begin{array}{*{20}{c}}
n\\
k+1
\end{array}} \right)}\)
Grâce à cette elle, on peut déterminer tous les coefficients binomiaux à l’aide d’une table dont la construction est simple : le triangle de Pascal, qui commence ainsi...
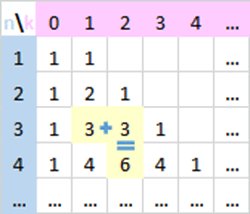
Ci-dessus est illustrée l’égalité suivante :
\({\left( {\begin{array}{*{20}{c}}
3\\
1
\end{array}} \right)} + {\left( {\begin{array}{*{20}{c}}
3\\
2
\end{array}} \right)}\) \(=\) \({\left( {\begin{array}{*{20}{c}}
4\\
2
\end{array}} \right)}\) \(=\) \(3 + 3\) \(=\) \(6\)
Représentation graphique
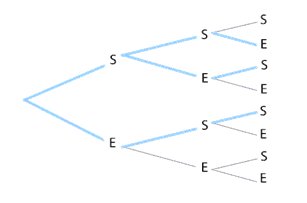
En d’autres termes, si l’on dessine l’arbre de dénombrement pour trouver « 2 parmi 4 », donc un arbre à quatre niveaux, on trouve six chemins qui satisfont à notre condition. Ces six chemins apparaissent au quatrième niveau, à l’extrémité de l’arbre. On peut les scinder en deux types, selon le profil qu’ils présentent au troisième niveau : il y a ceux qui comprenaient déjà les deux succès parmi trois et qui apparaissent en bleu ci-dessous (et il faut qu’à la dernière épreuve, ce soit un échec) et ceux qui n’enregistraient qu’un seul succès (non mis en exergue ci-dessous ; il leur faut le succès manquant lors de la quatrième épreuve).
Ci-dessous, les six chemins pour lesquels on relève deux succès et deux échecs sont représentés par les chemins bleus et les chemins rouges.
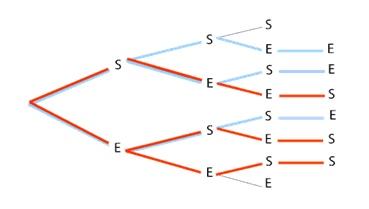
Plus généralement, si l’on souhaite déterminer le nombre de chemins pour lesquels il existe \(k + 1\) succès dans un schéma de Bernoulli à \(n + 1\) répétitions, alors ce nombre est la somme de deux termes qui s’expriment par des coefficients binomiaux. Si la \((n + 1)\)e épreuve est un succès, il doit y avoir eu précédemment \(k\) succès parmi \(n\) et si la \((n + 1)\)e épreuve est un échec, les \(k + 1\) succès ont dû apparaître au cours des \(n\) répétitions précédentes.
Logique, non ?
Utilisations
On peut simplement chercher un nombre de possibilités. Il s’agit d’une problématique de dénombrement. Mais c’est aussi dans le cadre probabiliste que le coefficient binomial trouve toute son utilité.
Si dans un schéma de Bernoulli on affecte des probabilités aux évènements, la représentation du schéma prend la forme d’un arbre pondéré. La variable aléatoire \(X\) égale au nombre de succès suit une loi de probabilité appelée loi binomiale. Pour déterminer la probabilité de \(X,\) on a besoin du coefficient binomial.
Et avec une calculatrice ?
Avec une TI : voir la loi binomiale avec TI.
Avec une Casio : retrouvons notre combinaison de 2 parmi 4. Touche MENU puis choix 1 (RUN-MAT). Entrez la valeur de \(n\), donc 4, puis touche OPTN. Choix PROB (F6 puis F3). Puis choix nCr (encore F3). Enfin la valeur de \(k,\) c'est-à-dire 2. EXE.

