Quelques graphiques avec R de base
Il est pratique d’utiliser R pour réaliser des graphiques, surtout avec R-Studio. Ici nous examinerons la fonction plot(). Comme nous le verrons, elle est assez polyvalente (moins qu’un smartphone mais bon, tout de même…).
Types de graphiques
La fonction plot() permet de réaliser les graphiques suivants :
- Des courbes qui relient des points d’observation. Pour les courbes mathématiques, on utilise plutôt la fonction curve() car plot() restitue une succession de lignes. Vous pourrez le constater ci-après puisque, pour ne pas alourdir cette page avec des données, nos exemples s’appuieront sur une fonction mathématique.
- Des graphiques en barres.
- Des nuages de points (voir les nuages de points avec R).
Syntaxe
plot(x, y, type = "p", col = "black", main = "Titre", xlab = "Axe X", ylab = "Axe Y")
Les principaux arguments sont les suivants :
- x, y : données à représenter (vecteurs).
- type : type de graphique (points, lignes, etc.).
- col : couleur des points/lignes (détaillé en page de graphiques avec R).
- main : titre du graphique (idem).
- xlab, ylab : titres des axes.
- pch : forme des points.
- lwd : épaisseur des lignes.
- lty : styles de lignes (1 = continue, 2 = tirets, 3 = pointillés, 4 = traits et points).
- xlim, ylim : limites des axes.
Les types sont l pour les lignes, h pour les barres, p pour les nuages de points, b pour des lignes avec des points, s pour des marches, o pour des points et des lignes superposées et n pour aucun tracé (prépare juste le cadre du graphe).
Les formes de points (pch) sont 0 (carré vide), 1 (cercle, c’est l’option par défaut), 2 (triangle pointant vers le haut), 3 (croix en forme de +), 4 (X), 5 (losange vide), 6 (triangle pointant vers le bas), 7 (X dans carré), 8 (étoile), 9 (losange avec croix), 10 (cercle avec croix), 11 (étoile à six branches), 12 (carré avec croix), 13 (cercle + carré + X), 14 (triangle dans carré), 15 (carré plein), 16 (disque), 17 (triangle plein pointant vers le haut), 18 (losange plein), 19 (disque épais), 20 (petit disque), 21 (disque avec bord et couleur de remplissage), 22 (idem en carré), 23 (idem en losange), 24 (idem avec triangle pointant en haut) et 25 (idem avec triangle pointant en bas). Les formes 3, 8 et 11 sont illustrées en page de nuages de points.
Lignes et grille
La fonction abline() permet d’obtenir des traits horizontaux ou verticaux, voire les deux pour réaliser une grille. Les arguments sont h (horizontal), v (vertical) et l’espacement. Voir les exemples ci-dessous. Notez qu'abline() offre beaucoup d'autre possibilités (voir la droite d'ajustement).
Exemples
Pour observer les effets obtenus, nous utiliserons la fonction racine carrée.
x <- 1:5
y <- sqrt(x)
Sans autre argument que le type de graphique, la succession de lignes apparaît ainsi :
plot(x, y, type = "l", main = "Lignes (l)")
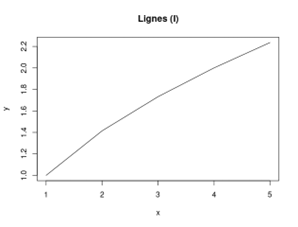
À présent, nous souhaitons que cette « courbe » soit plus épaisse et de couleur grenat, avec des lignes horizontales bleues et des points carrés.
plot(x, y, type = "b", main = "Lignes (l)", col = "darkred", lwd = 3, pch = 7)
abline(h = seq(1, 2.2, by = 0.2), col = "blue", lty = 1)
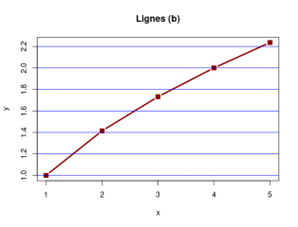
Si l’on opte pour type = "o" (profitons-en pour dessiner les lignes horizontales en pointillés), la différence n’est pas énorme mais l’apparence du graphique est plus classique.
plot(x, y, type = "o", main = "Lignes (o)", col = "darkred", lwd = 3, pch = 7)
abline(h = seq(1, 2.2, by = 0.2), col = "blue", lty = 3)
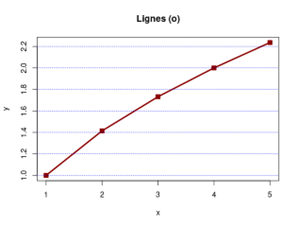
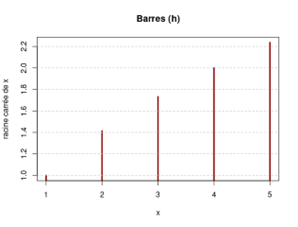
Passons aux barres verticales. Plus besoin de définir une forme de point ! Cette fois, nos lignes horizontales sont en tirets gris et nous avons ajouté un nom à l’axe des ordonnées.
plot(x, y, type = "h", main = "Barres (h)", col = "darkred", lwd = 3, ylab = "racine carrée de x")
abline(h = seq(1, 2.2, by = 0.2), col = "grey", lty = 2)
Avec une variable qualitative, voir l'exemple en page de facteurs (barres larges).
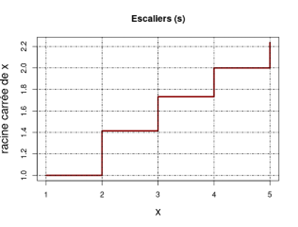
Maintenant, les marches avec lty = 4, l’ajout de lignes verticales pour obtenir une grille et l’agrandissement des titres d’axes.
plot(x, y, type = "s", main = "Escaliers (s)", col = "darkred", lwd = 3, ylab = "racine carrée de x", cex.lab = 1.5)
abline(h = seq(1, 2.2, by = 0.2), lty = 4)
abline(v = seq(1, 5, by = 1), lty = 4)
Vous avez compris que le graphe est faux puisque la fonction racine carrée est continue sur l’intervalle considéré. Peu importe, le but est juste d’illustrer une possibilité de plot.