Tests et intervalles de prévision sur une régression
Vous venez d’obtenir une équation de régression linéaire simple (RLS) ou multiple. Le coefficient de détermination vous donne une indication sur la qualité globale du modèle. Peut-on aller plus loin et valider les paramètres pris séparément ? La réponse est oui.

Les tests
Pour tester la pertinence de chaque paramètre (coefficient(s) et constante de régression), diverses hypothèses sont émises sur les erreurs de mesure dont sont entachées les observations. Elles représentent une part d’aléa qui se répercutera sur les paramètres du modèle dont l’exactitude dépend évidemment de la qualité des données. On ne validera pas ces hypothèses puisqu’on ignore toujours quelles erreurs ont été commises, sauf peut-être si l’on pratique la radiesthésie sur les tableaux de données (méthode non admise par la communauté des data analysts). Attention : ne pas confondre ce type d’erreur avec les résidus du modèle qui, eux, sont connus.
Les hypothèses sont celles de variances identiques et indépendantes des erreurs ainsi que de leurs distributions normales.
Situons-nous d’abord dans le cadre d’une RLS. Le modèle apparaît sous cette forme bien connue : \({\widehat{y}_i} = \widehat a{x_i} + \widehat b + {\varepsilon _i}\)
Le premier paramètre à tester est le coefficient directeur de la droite des moindres carrés qui indique sa pente. Si ce coefficient est nul, la droite est horizontale, montrant par là son incapacité à résumer un nuage de points. Pour une RLS, ce test est équivalent à un test de nullité du coefficient de détermination \(R^2\) (test du F). Si la régression est multiple, chaque coefficient doit être testé pour être admis dans le modèle. Le second paramètre est bien sûr la constante de régression.
L’hypothèse nulle du test est que le paramètre \(a\) ou \(b\) est égal à zéro. L’hypothèse alternative H1 est celle que l’on espère être la bonne, le paramètre méritant sa place dans l’équation avec la valeur qu’on lui a trouvée. La mise en œuvre est possible puisqu’on a préalablement estimé des variances pour \(a\) et pour \(b\) (voir les coefficients de la régression).
Ces tests, bilatéraux, sont réalisés avec un t de Student. Un test z utilisant la loi normale supposerait que la vraie variance des erreurs est connue, ce qui est rarissime, ou que les données sont très nombreuses (rare également).
Sous H0, la différence entre l’estimateur d’un paramètre et zéro (donc, l’estimateur seul ; la soustraction n’est pas très difficile…), divisée par l’écart-type de ce même paramètre, est inférieure à la valeur du t à \(n - 2\) degrés de liberté (\(n - 3\) pour une régression multiple à deux coefficients, etc.).
Les intervalles de confiance
Comme des tests sont réalisés sur les paramètres de la régression, il est possible d’établir des intervalles de prévision probabilisés. Appelons \(σ^2\) la variance des résidus. On peut prévoir la variance de l’erreur de l’observation à venir \(n + 1,\) qui est aussi la variance de notre estimateur de \(y\) en \(n + 1.\)
\({\rm{Var}}({\varepsilon _{n + 1}})\) \(=\) \(\displaystyle{{\sigma ^2}\left[ {1 + \frac{1}{n} + \frac{{{{({x_{n + 1}} - \overline x )}^2}}}{{\sum {{{({x_i} - \overline x )}^2}} }}} \right]}\)
Les bornes de l’intervalle de prévision sont donc \({\widehat y_i} \pm {t_{\frac{\alpha }{2},n - 2}} \times {\sigma _{\widehat yi}}\)
Exemple
Illustrons par une régression multiple. Les données sont celles de la page d'exemple de RLM dont voici en quelque sorte le prolongement.
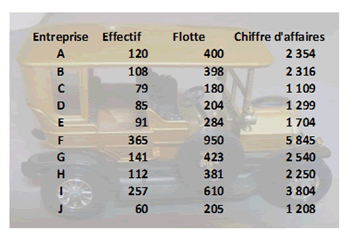
Le logiciel Statistica nous fournit les résultats suivants.
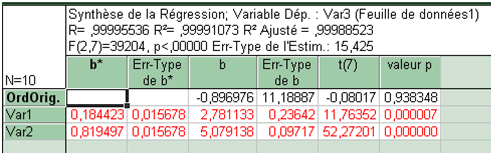
Nous nous intéressons aux cinquième et sixième colonnes. Les valeurs des deux coefficients peuvent être retenues. En revanche, on ne peut pas rejeter H0 lorsque le test est effectué sur la constante de régression. La probabilité de se situer au-delà de n’importe quel intervalle de confiance est trop élevée (0,938).
En complément à la sortie de Statistica, voyons de plus près certains éléments. Par exemple, le t de 11,76 pour le coefficient de la première variable (l’effectif). Comment le construit-on ? Au numérateur se trouve l’estimateur, donc 2,78, qui est divisé par son écart-type, donc 0,236. La statistique obtenue s’établit à 11,763.
Dans la table du t, la ligne que nous retenons est la septième (7 degrés de liberté). Si le risque d’erreur choisi est \(5\%,\) on lit dans la table 2,365. C’est une valeur très inférieure à 11,763. Nous sommes donc largement en-dehors de l’intervalle dans lequel le coefficient peut être considéré nul. Le logiciel nous donne une p-value peu différente de zéro qu’on ne trouve pas dans la table tant 11,763 est une valeur élevée…
Graphiquement, une régression multiple ne serait pas très lisible. Devrons-nous nous passer de l’intervalle de prédiction que vous attendez tous ? Non, Statistica autorise tout de même quelques représentations. En voici une qui permet, pour un intervalle de confiance de \(95\%,\) de visualiser les résidus (option Val. Prévues vs. Résidus) :
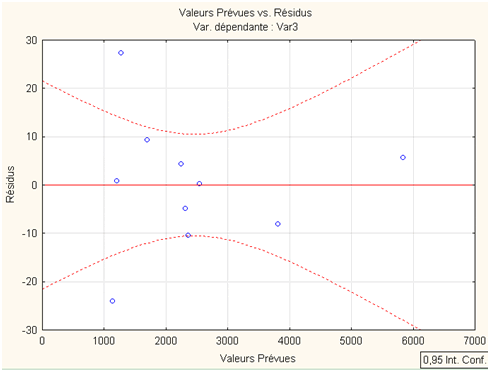
Il y a tout de même deux entreprises (C et D) pour lesquelles la régression laisse des résidus en-dehors de l’intervalle de prévision…
