Intervalles de prédiction non probabilisés
Une technique de régression, la forme linéaire simple est largement enseignée. Mais on peut affiner...
Problématique
Soit une distribution bivariée : on soupçonne une liaison entre les variables quantitatives et, à partir de l’une qui est connue, on cherche à déterminer la valeur de l’autre. Graphiquement, cette liaison prend la forme d'une droite représentative d'une fonction affine \((y = ax + b)\) qui traverse un nuage de points.
Ainsi, une équation doit permettre de prédire la valeur prise par une variable à expliquer \(y.\) Mais la prédiction (ou la prévision s’il s’agit d’un modèle temporel) ne sera exacte qu’avec l’heureux concours d’un magnifique coup de chance puisqu’on cherche à prédire une valeur prise par une variable aléatoire. On risque donc de taper à côté, d’une part parce qu’un aléa peut réellement exister (erreur de mesure, notamment) et d’autre part parce qu’un modèle imparfait générera la présence d’un résidu pour chaque valeur observée ou prédite. Les paramètres du modèle comme les valeurs prédites ont donc tous une variance.
Par conséquent, la droite des moindres carrés qui résume l’équation du modèle peut bouger, du moins à l’intérieur d’un intervalle d’autant plus resserré que le modèle en question est fiable.
L’objectif de cette page est de montrer ce qu’est un intervalle de prédiction, sans considérations probabilistes. Nous nous appuierons sur la régression simple mais les explications valent aussi bien pour la régression multiple.
Il faut d’abord avoir en tête que la droite des moindres carrés (DMC), qui permet de résumer au mieux le nuage de points des observations, passe nécessairement par le centre de gravité du nuage, c’est-à-dire par un point moyen qui ne correspond presque jamais à une observation (moyenne des abscisses et moyenne des ordonnées).
L’ordonnée de ce point moyen est aléatoire. En d’autres termes, l’espérance de y a une variance non nulle. On peut la visualiser ainsi :
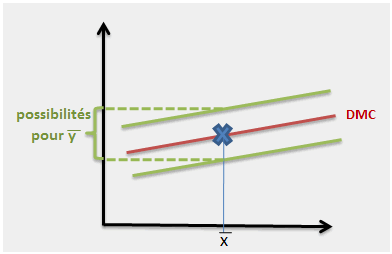
On a là un premier critère de qualité. Plus la droite de régression a de la place pour zigzaguer, moins le modèle est prédictif. On peut par exemple voir des points assez bien alignés (coefficient de corrélation proche de 1) mais tellement peu d’observations que le modèle est malgré tout inexploitable…

Après les zigzags, la balançoire. Supposons maintenant que le point moyen est correctement fixé. Les paramètres de la droite sont eux aussi aléatoires, c’est-à-dire que la droite peut plus ou moins pivoter autour du centre de gravité (les deux paramètres sont de toute façon liés par une covariance négative : si \(a\) augmente, \(b\) diminue et réciproquement).
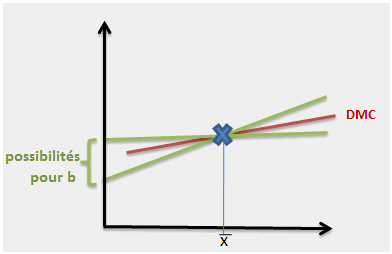
C’est là le second critère de qualité, bien compréhensible lui aussi, évalué par le coefficient de corrélation et le \(R^2\).
Illustration
Mixons à présent ces deux critères. On arrive évidemment à un graphe de ce type :
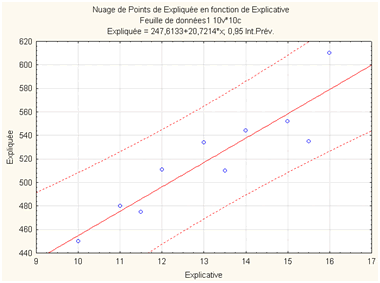
Cette illustration, obtenue avec Statistica, a été réalisée à partir des données suivantes :

On constate que les enveloppes de cet intervalle de prévision sont courbes, évidemment à cause du second critère. Question de bon sens, du moins dans la version temporelle de la régression : plus l’échéance de la prévision est lointaine, moins elle est sûre. En revanche, au centre du nuage, l’intervalle est le plus étroit puisqu’il n’intègre que le premier critère.
En d’autre termes, plus on s’éloigne du point moyen, plus la variance de l’erreur par rapport au modèle est conséquente. D’ailleurs, comment est-elle déterminée ?
\[{\rm{Var}}\left( {{\varepsilon _{n + 1}}} \right) = {\sigma ^2}\left[ {1 + \frac{1}{n} + \frac{{{{\left( {{x_{n + 1}} - \overline x } \right)}^2}}}{{\sum {{{\left( {{x_i} - \overline x } \right)}^2}} }}} \right]\]
\(\sigma^2\) est la variance des résidus. Nul besoin d’être surdoué en maths pour s’apercevoir que plus \(n\) est éloigné de la moyenne des \(x\) et plus la variance des erreurs est élevée. Et la variance de l’erreur est bien sûr la même que celle de \(y\) (couloir du graphe n° 1).
Si de plus on considère que la distribution des erreurs est normale, il devient possible de probabiliser l’intervalle, par exemple en établissant les frontières à l’intérieur desquelles on a 95 chances sur 100 d’observer \(y_i\) pour un \(x_i\) que l’on s’est donné. Épatant, non ?
Mais ceci est une autre histoire, racontée en page tests sur les paramètres d’une régression. Vous y trouverez aussi le moyen de visualiser l’intervalle de prévision d’une régression multiple.
