Exercices sur l'encodage des nombres
Le programme de première de NSI n’est pas toujours très précis. Et du coup, les manuels et ouvrages extra-scolaires ont des contenus assez différents d’un éditeur à l’autre. Certains sont très accessibles tandis que d’autres ne sont pas vraiment adaptés à des élèves de première, même hyper motivés (à notre humble avis).
Nous vous proposons ici quelques exercices sur la représentation des nombres. Comme ce n’est pas le thème le plus enthousiasmant du programme (là encore, avis personnel), ces exercices ne seront pas très difficiles.
Exercice 1 : opérations sur entiers
La réalisation de cet exercice suppose que l’encodage des entiers est bien maîtrisé.
Calculer à la façon de l’unité arithmétique et logique d’un ordinateur (sur huit bits) :
- \(23 + 60\)
- \(50 - 20\)
Corrigé
- En base 2, 23 s’écrit 10111 car c’est la somme de \(2^4,\) \(2^2,\) \(2^1\) et \(2^0.\) Quant à 60, c’est 111100.
-
Additionnons. Rappelons qu’en base 2, \(1 + 1 = 10\) (donc on pose 0 et on retient 1)
| Retenue | 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | |
| + | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| = | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
- En base 10, 1010011 vaut \(2^6 + 2^4 + 2^1 + 2^0\) soit 83.
- Pour effectuer la soustraction, nous additionnons \(50 + (-20).\)
- 50 en base 2 s’écrit 110010.
20 s’écrit 10100 donc sur un octet -20 s’écrit \(10001011 + 1\) \(=\) \(11101100.\)
| Retenue | 1 | 1 | ||||||
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | |
| + | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| = | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
- Et 00011110 est bien la traduction de \(+30.\)

Exercice 2 : base 16
- La base 16 trouve plusieurs utilisations en informatique. Traduire les entiers naturels trouvés à l’exercice précédent, c’est-à-dire 83 et 30, en base 16.
- Écrire ensuite un milliard en base 16 (seul matériel autorisé : une calculatrice sans Python).
Rappel : pour écrire un nombre en base 16 il nous faut seize chiffres (de 0 à 15). Or nous n’en avons que dix à notre disposition. Les « chiffres » compris entre 10 et 15 sont donc les suivants :
| 10 | A |
| 11 | B |
| 12 | C |
| 13 | D |
| 14 | E |
| 15 | F |
Corrigé
- \(83 = 5 \times 16^1 + 3 \times 16^0.\) Donc la traduction en base 16 de 83 est 53.
- Vérification avec Python :
- >>> hex(83)
'0x53'
- Notez que ce résultat apparaît comme une chaîne de caractères dons les deux premiers (0x) indiquent que le nombre qui suit est en hexadécimal.
- \(30 = 16^1 + 14 \times 16^0\) soit 1E puisque la traduction de 14 est E.
- Comment écrire un milliard, soit \(10^9,\) en base 16 ?
- Avec la calculatrice, nous constatons que ce nombre est compris entre \(16^7\) et \(16^8.\)
- \(16^7 = 268\,435\,456.\) Division euclidienne d’un milliard par ce nombre. On trouve 3 et un reste de 194 493 632.
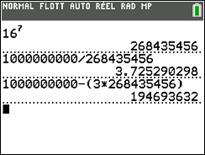
- \(\frac{194\,693\,632}{16^6} = 11\) et un reste de 10 144 256.
\(\frac{10\,144\,256}{16^5} = 9\) et un reste de 707 072.
\(\frac{707\,072}{16^4} = 10\) et un reste de 51 712.
\(\frac{51\,712}{16^3} = 12\) et un reste de 2 560.
\(\frac{2\,560}{16^2} = 10\) et il n’y a pas de reste. Donc \(16^1\) et \(16^0\) se traduiront par des zéros.
- Un milliard en hexadécimal s’écrit donc 3B9ACA00. Vérifions-le avec Python :
- >>> hex(1000000000)
'0x3b9aca00'
Exercice 3 : arrondis
En page d’encodage des réels, il est montré qu’un nombre fini de bits pour encoder des nombres avec décimales peut conduire à des approximations, voire des erreurs.
Vérifier avec Python si \(10 \times \frac{1}{3} = \frac{10}{3}.\)
Corrigé
La vérification est vite faite. Inutile d’écrire un long programme, une ligne sur la console suffit !
>>> 10/3 == 3 * (1/3)
False
Il suffit d’ailleurs d’entrer \(\frac{10}{3}\) pour constater que le flottant est inexact.
>>> 10/3
3.3333333333333335
Pour vérifier informatiquement une égalité entre flottants, il est préférable de montrer que la différence entre leurs valeurs absolues est inférieure à un nombre très petit. Ici, avec une précision de \(10^{-15}\) on considère qu’il y a égalité.
>>> abs(10/3) - abs(10 * (1/3)) < 1e-15
True
