Construction d'une table du t de Student
Non seulement vous avez ci-dessous une table du \(t\) de Student mais en prime vous pourrez la refaire vous-même avec Excel (du moins si la version n’est pas trop ancienne). Que demander de plus ?
Lorsqu’une variable aléatoire \(T\) suit une loi de Student pour un nombre donné de degrés de liberté (ddl) \(\nu,\) on cherche la valeur de \(t\) pour laquelle la probabilité que \(T\) se situe entre \(-t\) et \(t\) est égale à un certain pourcentage. Comme il est beaucoup moins fréquent de chercher \(p[T < t],\) nous construirons la table des valeurs de \(t\) pour \(f(t) = 1 - \frac{α}{2}\) donné (\(α\) étant le risque d’être dépassé de part et d’autre de la distribution).
Avec Excel
La fonction à utiliser est =LOI.STUDENT.INVERSE.BILATERALE.
Indiquez en colonne le nombre de ddl selon votre convenance et en ligne les probabilités d’être dépassées, également selon votre convenance.
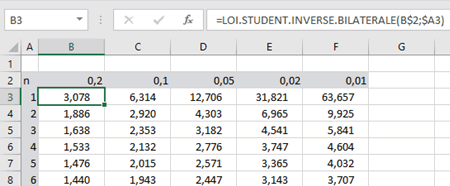
Si vous devez aussi effectuer des tests unilatéraux, il est commode de diviser \(α\) par 2 dans la même table.
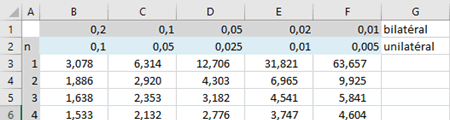
Table
Valeurs de \(t\) ayant la probabilité \(α\) d’être dépassées en valeur absolue.
| ν\α | 0,2 | 0,1 | 0,05 | 0,02 | 0,01 |
|---|---|---|---|---|---|
| 1 | 3,078 | 6,314 | 12,706 | 31,821 | 63,657 |
| 2 | 1,886 | 2,920 | 4,303 | 6,965 | 9,925 |
| 3 | 1,638 | 2,353 | 3,182 | 4,541 | 5,841 |
| 4 | 1,533 | 2,132 | 2,776 | 3,747 | 4,604 |
| 5 | 1,476 | 2,015 | 2,571 | 3,365 | 4,032 |
| 6 | 1,440 | 1,943 | 2,447 | 3,143 | 3,707 |
| 7 | 1,415 | 1,895 | 2,365 | 2,998 | 3,499 |
| 8 | 1,397 | 1,860 | 2,306 | 2,896 | 3,355 |
| 9 | 1,383 | 1,833 | 2,262 | 2,821 | 3,250 |
| 10 | 1,372 | 1,812 | 2,228 | 2,764 | 3,169 |
| 11 | 1,363 | 1,796 | 2,201 | 2,718 | 3,106 |
| 12 | 1,356 | 1,782 | 2,179 | 2,681 | 3,055 |
| 13 | 1,350 | 1,771 | 2,160 | 2,650 | 3,012 |
| 14 | 1,345 | 1,761 | 2,145 | 2,624 | 2,977 |
| 15 | 1,341 | 1,753 | 2,131 | 2,602 | 2,947 |
| 16 | 1,337 | 1,746 | 2,120 | 2,583 | 2,921 |
| 17 | 1,333 | 1,740 | 2,110 | 2,567 | 2,898 |
| 18 | 1,330 | 1,734 | 2,101 | 2,552 | 2,878 |
| 19 | 1,328 | 1,729 | 2,093 | 2,539 | 2,861 |
| 20 | 1,325 | 1,725 | 2,086 | 2,528 | 2,845 |
| 21 | 1,323 | 1,721 | 2,080 | 2,518 | 2,831 |
| 22 | 1,321 | 1,717 | 2,074 | 2,508 | 2,819 |
| 23 | 1,319 | 1,714 | 2,069 | 2,500 | 2,807 |
| 24 | 1,318 | 1,711 | 2,064 | 2,492 | 2,797 |
| 25 | 1,316 | 1,708 | 2,060 | 2,485 | 2,787 |
| 26 | 1,315 | 1,706 | 2,056 | 2,479 | 2,779 |
| 27 | 1,314 | 1,703 | 2,052 | 2,473 | 2,771 |
| 28 | 1,313 | 1,701 | 2,048 | 2,467 | 2,763 |
| 29 | 1,311 | 1,699 | 2,045 | 2,462 | 2,756 |
| 30 | 1,310 | 1,697 | 2,042 | 2,457 | 2,750 |
| 31 | 1,309 | 1,696 | 2,040 | 2,453 | 2,744 |
| 32 | 1,309 | 1,694 | 2,037 | 2,449 | 2,738 |
| 33 | 1,308 | 1,692 | 2,035 | 2,445 | 2,733 |
| 34 | 1,307 | 1,691 | 2,032 | 2,441 | 2,728 |
| 35 | 1,306 | 1,690 | 2,030 | 2,438 | 2,724 |
| 36 | 1,306 | 1,688 | 2,028 | 2,434 | 2,719 |
| 37 | 1,305 | 1,687 | 2,026 | 2,431 | 2,715 |
| 38 | 1,304 | 1,686 | 2,024 | 2,429 | 2,712 |
| 39 | 1,304 | 1,685 | 2,023 | 2,426 | 2,708 |
| 40 | 1,303 | 1,684 | 2,021 | 2,423 | 2,704 |
| 50 | 1,299 | 1,676 | 2,009 | 2,403 | 2,678 |
| 60 | 1,296 | 1,671 | 2,000 | 2,390 | 2,660 |
| 70 | 1,294 | 1,667 | 1,994 | 2,381 | 2,648 |
| 80 | 1,292 | 1,664 | 1,990 | 2,374 | 2,639 |
| 90 | 1,291 | 1,662 | 1,987 | 2,368 | 2,632 |
| 100 | 1,290 | 1,660 | 1,984 | 2,364 | 2,626 |
| 150 | 1,287 | 1,655 | 1,976 | 2,351 | 2,609 |
| 200 | 1,286 | 1,653 | 1,972 | 2,345 | 2,601 |
| 250 | 1,285 | 1,651 | 1,969 | 2,341 | 2,596 |
| 300 | 1,284 | 1,650 | 1,968 | 2,339 | 2,592 |
| 350 | 1,284 | 1,649 | 1,967 | 2,337 | 2,590 |
| 400 | 1,284 | 1,649 | 1,966 | 2,336 | 2,588 |
| 500 | 1,283 | 1,648 | 1,965 | 2,334 | 2,586 |
| 1000 | 1,282 | 1,646 | 1,962 | 2,330 | 2,581 |
| 2000 | 1,282 | 1,646 | 1,961 | 2,328 | 2,578 |
| 5000 | 1,282 | 1,645 | 1,960 | 2,327 | 2,577 |
En lecture verticale de la table, on constate que la dispersion est plus élevée que pour une loi normale et qu’un intervalle de confiance établi avec la loi de Student est donc plus large. Plus l’effectif (ou le nombre de ddl) est petit et plus la variance sans biais est incertaine, plus les valeurs sont dispersées. Ce qui se traduit par une courbe de densité de probabilité davantage écrasée. En revanche, plus le nombre de ddl augmente, plus la loi de Student converge vers la loi normale. On remarque d’ailleurs que la valeur de \(t\) pour un échantillon très grand et pour un risque d’erreur de 0,05 (donc 0,025 de chaque côté de la distribution) est égale à 1,96, valeur bien connue lorsqu’on utilise la loi normale centrée réduite…
