Suite arithmétique : rappels et somme de termes
Vous savez ce qu’est une suite arithmétique. Bravo. Maintenant, on risque fort de vous demander non seulement d’en calculer des termes mais aussi de les additionner. Et attention, pas de façon artisanale mais avec une formule. C’est l’objet de cette page. Comme cette opération figure dans les programmes des élèves de première générale et des terminales technologiques, elle s’adresse à un large public. Il y a quelques petites différences d’approche qui seront signalées, mais rien de bien méchant.
Rappels sur les suites arithmétiques
Lorsqu’on ajoute ou que l’on soustrait toujours le même nombre pour passer d’un terme de la suite au suivant, il s’agit d’une suite arithmétique. Ce nombre est appelé la raison.
Soit \((u_n)\) une suite arithmétique de premier terme \(u_0\) et de raison \(r.\)
On peut la définir par récurrence : on donne la valeur de \(u_0\) et on on pose \(u_{n+1} = u_n + r.\)
On peut aussi la définir par une formule qui donne directement la valeur du terme sans avoir à calculer tous les précédents. C’est le terme général.
Par exemple, si l’on cherche la raison d’une suite arithmétique sachant que \(u_0 = 10\) et \(u_1 = 12,\) on la trouve en soustrayant \(12 - 10 = 2.\)
Autre exemple, si l’on cherche la raison et le premier terme \(u_0\) d’une suite arithmétique sachant que \(u_4 = 5\) et \(u_6 = 11\), on commence par trouver la raison : comme elle apparaît deux fois entre les rangs 4 et 6, on a \(11 - 5 = 2r.\) D’où \(r = 3.\) Celle-ci apparaît quatre fois entre \(u_0\) et \(u_4\) donc \(u_0 + 4 × 3 = 5\) et \(u_0\) est donc égal à \(5 - 12 = -7.\)
Graphiquement, une suite arithmétique est représentée par des points alignés dans un repère.
Somme des termes
La somme des quatre premiers termes peut s’écrire \(S\) \(=\) \(u_0 + u_1 + u_2 + u_3.\) Donc attention au décalage si la suite commence au rang zéro.
En terminale technologique cette somme s’écrit \(\sum\limits_{i = 0}^3 {{u_i}} \) (somme des \(u_i\) de 0 à 3). Le symbole de la somme (qui est la lettre grecque sigma majuscule) est très souvent utilisé en statistiques (voir la page d'initiation à la dispersion).
La somme des termes consécutifs d’une suite arithmétique est la moyenne du premier et du dernier terme (donc leur somme divisée par 2), multipliée par le nombre de termes.
Ainsi si le premier terme est \(u_0\) la somme des \(n + 1\) premiers termes est :
\(S = (n + 1) \frac{u_0 + u_n}{2}\)
Si le premier terme est \(u_1\) alors la somme des \(n\) premiers termes est :
\(S = n × \frac{u_1 + u_n}{2}\)
Exemple
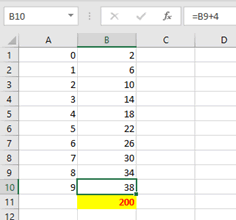
Soit la suite \((u_n)\) définie par \(u_0 = 2\) et \(r = 4.\) Déterminons la somme des dix premiers termes.
Première chose : on doit calculer \(u_9\) car c’est lui le dixième terme. Pour le trouver, on part de \(u_0\) et on ajoute neuf fois la raison. Donc \(2 + 9 × 4 = 38.\) Ensuite, la raison ne nous sert plus puisqu’elle ne figure pas dans la formule (si vous respectez bien le tri sélectif, vous pouvez la jeter dans le bac réservé aux raisons).
Deuxième étape, la formule :
\(\sum\limits_{i = 0}^9 {{u_i}}\) \(=\) \(10 \times \frac{{{u_0} + {u_9}}}{2}\) \(=\) \(10 \times \frac{{2 + 38}}{2}\) \(=\) \(200\)
On peut vérifier très facilement ce résultat avec un tableur.
Et avec Python ?
Python
Avec un algorithme, il est inutile de passer par la formule et de calculer le dernier terme. On se sert du même mécanisme que ci-dessus avec Excel, c’est-à-dire que l’on calcule tous les termes avant de les additionner. D’accord, c’est un peu primaire. Mais avec la puissance de l’informatique, ce n’est pas gênant.

Les valeurs de trois variables sont saisies par l’utilisateur. La variable \(s\) (qui est la somme des \(n\) premiers termes) est définie « à la volée » dans la fonction. Elle est initialisée en \(u,\) qui est alors le premier terme (sinon la somme l’oubliera). La boucle bornée tourne \(n\) fois, de 0 à \(n - 1.\) Chaque valeur de \(u\) écrase la précédente. Idem pour les valeurs de \(s.\)
Exercice corrigé
Tom décide de pratiquer le ski de fond. Lundi, il parcourt 6 km. Puis chaque jour il skie sur une distance majorée de 500 m par rapport à la veille. Sur quelle distance skie-t-il le lundi suivant ? Combien de kilomètres a-t-il parcouru au cours de ces huit jours ?

Comme sa progression quotidienne est toujours de 0,5 km, on peut modéliser la distance parcourue chaque jour par une suite arithmétique \((u_n)\) de raison 0,5 et de premier terme \(u_0 = 6.\)
Le lundi suivant correspond à \(u_7 = 6 + 7 × 0,5\) \(=\) \(9,5.\) Ce jour-ci, il skie sur 9,5 km.
En huit jours, il aura skié \(8 × \frac{6 + 9,5}{2} = 62\) km.
Il ne vous reste plus qu'à vous diriger vers la page traitant de la somme de termes d'une suite géométrique...
